Chapter 2. Simple and Compound Statements

Irving M. Copi, Symbolic Logic, New York: Macmillan Publishing, 1979, pp. 8-14.

 

(1) Simple and Compound Statements

① simple and compound

(a) All statements can be divided into two kinds, simple and compound.

A simple statement	A compound statement
does not contain any other statement as a component part	does contain another statement as a component part

For example, ‘Atmospheric testing of nuclear weapons will be discontinued or this planet will become uninhabitable' is a compound statement that contains, as its components, the two simple statements ‘Atmospheric testing of nuclear weapons will be discontinued and ‘this planet will become uninhabitable’. The component parts of a compound statement may themselves be compound, of course.

(b) 'The third wife of Bertrand Russell was a beautiful girl,' can be regarded as a statement in its own right. But it is not a component part or a component of the larger statement containing it.

For a part of a statement to be a component of a larger statement, two conditions must be satisfied.
First, the part must be a statement in its own right; and second, if the part is replaced in the larger statement by any other statement, the result of that replacement must be meaningful.

Although the first condition is satisfied in the example given, the second is not. For if the part Bertrand Russell was a beautiful girl is replaced by the statement ‘Where there’s smoke, there’s fire’, the result of that replacement is arrant nonsense.

 

② truth-functional

(a) Everv statement is either true or false, so we can speak of the truth value of a statement, where the truth value of a true statement is true and the truth value of a false statement is false. There are two broad categories into which compound statements can be divided, according to whether or not there is anything other than the truth values of its component statements that determines the truth value of the compound statement. The truth value of the conjunction of two statements is completely determined by the truth value of its conjuncts. A conjunction is true if both its conjuncts are true, but false otherwise. For this reason a conjunction is a truth-functional compound statement, and its conjuncts are truth-functional components of it.

(b) Not every compound statement is truth-functional. For example, the truth-value of the compound statement ‘Percival Lowell believed that Mars is inhabited’ is not in any way determined by the truth value of its component simple statement ‘Mars is inhabited’. This is so because it could be true that Percival Lowell believed that Mars is inhabited, regardless of whether it is inhabited or not. A person can believe one truth without believing another, and a person can believe one falsehood without believing all of them. So the component ‘Mars is inhabited is not a truth-functional component of the compound statement Percival Lowell believed that Mars is inhabited, and the latter statement is not a truth-functional compound statement.

(c) We define an occurrence of a component of a compound statement to be a truth-functional component of that compound statement provided that: If that occurrence of the component is replaced in the compound (or in any component of the compound statement which contains the component in question) by different statements that have the same truth value as each other, the different compound statements produced by these replacements will also have the same truth values as each other.

(d) And now a compound statement is defined to be a truth-functional compound statement, if all of its components are truth-functional components of the statement.

(e) The only compound statements we shall consider here will be truth-functionally compound statements. Therefore, in the rest of this book we shall use the term "simple statement" to refer to any statement that is not truth-functionally compound.

 

③ conjunction

(a) The statement 'Roses are red and violets are blue' is a conjunction, a compound statement formed by inserting the word ‘and' between two statements. Two statements so combined are called conjuncts.

(b) The word ‘and' has other uses, however, as in the statement ‘Castor and Pollux were twins’, which is not compound, but a simple statement asserting a relationship. We introduce the dot • as a special symbol for combining statements conjunctively. Using this notation, the preceding conjunction is written ‘Roses are red • violets are blue’. Where p and q are any two statements whatever, their conjunction is written p • q.^[각주:1]

(c) Since conjunctions are truth-functionally compound statements, our dot symbol is a truth-functional connective. Given any two statements p and q there are just four possible sets of truth values they can have, and in every case the truth value of their conjunction p ∧ q is uniquely determined. The four possible cases can be exhibited as follows:

in case p is true and q is true, p ∧ q is true;
in case p is true and q is false, p ∧ q is false;
in case p is false and q is true, p ∧ q is false;
in case p is false and q is false, p ∧ q is false.

Representing the truth values true and false by the capital letters 'T' and 'F,' respectively, the way in which the truth value of a conjunction is determined by the truth values of its conjuncts can be displayed more briefly by means of a truth table as follows:

Since it specifies the truth value of p ∧ q in every possible case, this truth table can be taken as defining the dot symbol. Other English words such as ‘moreover’, ‘furthermore’, ‘but’, ‘yet’, ‘still’, ‘however’, ‘also’, ‘nevertheless’, ‘although’, and so forth, and even the comma and the semicolon, are also used to conjoin two statements into a single compound one, and all of them can be indifferently translated into the dot symbol, so far as truth values are concerned.

 

④ Negation

The statement 'It is not the case that lead is heavier than gold' is also compound, being the negation (or denial or contradictory) of its single component statement 'lead is heavier than gold.' We introduce the symbol , called a curl 곱슬 (or a tilde 물결표) to symbolize negation. There are often alternative formulations in English of the negation of a given statement. Thus where L symbolizes the statement 'lead is heavier than gold,' the different statements 'it is not the case that lead is heavier than gold,' 'it is false that lead is heavier than gold,' 'it is not true that lead is heavier than gold,' 'lead is not heavier than gold' are all indifferently symbolized as ~L. More generally, where p is any statement whatever, its negation is written ~p. Since the negation of a true statement is false and the negation of a false statement is true, we can take the following truth table as defining the curl symbol:

 

⑤ Disjunction

(a) When two statements are combined disjunctively by inserting the word ‘or' between them, the resulting compound statement is a disjunction (or alternation), and the two statements so combined are called disjuncts (or alternatives).

(b) Inclusive / Exclusive

Disjunction
Inclusive (or weak)	Exclusive (or strong)
‘and/or’	‘but not both'
at least one disjunct is true	at least one disjunct is true but not both are true
(p ∨ q)	(p ∨ q) ∧ ~(p ∧ q)

(c) Where p and q are any two statements whatever, their weak or inclusive disjunction is written p v q. The symbol ‘v’, called a wedge 쐐기 (or a vee v자형의 것), is a truth-functional connective, and is defined by the following truth table:

 

⑥ Punctuation

(a) The use of parentheses, brackets, and braces for punctuating mathematical expressions is familiar. In the absence of a special convention, no number is uniquely denoted by the expression '6 + 9 ÷ 3,' although when punctuation makes clear how its constituents are to be grouped, it denotes either 5 or 9.

(b) Punctuation is needed to resolve ambiguity in the language of symbolic logic too, since compound statements may themselves be combined to produce more complicated compounds. Ambiguity is present in p ∧ q ∨ r, which could be either the conjunction of p with q ∨ r, or else the disjunction of p ∧ q with r. These two different senses are unambiguously given by different punctuations: p ∧ (q ∨ r) and (p ∧ q) ∨ r. In case p and q are both false and r is true, the first punctuated expression is false (since its first conjunct is false), but the second punctuated expression is true (since its second disjunct is true).

(c) Here, a difference in punctuation makes all the difference between truth and falsehood. In symbolic logic, as in mathematics, we use parentheses^[각주:2], brackets^[각주:3], and braces ^[각주:4] for punctuation. To cut down on the number of punctuation marks required, however, we establish the symbolic convention that in any expression the curl will apply to the smallest component that the punctuation permits. Thus the ambiguity of ~p ∨ q, which might mean either (~p) ∨ q or ~(p ∨ q), is resolved, by our convention, to mean the first of these. The curl can, and therefore by our convention does, apply to the first component p rather than to the larger expression p ∨ q.

 

⑦ 'either,' 'neither,' 'both,' and 'unless'

Either...or...
Either Alice will be elected or Betty will be elected	Either Alice will be elected or Betty will be elected
Charlene will be either secretary or treasurer	Either Charlene will be secretary or Charlene will be treasurer

Neither...nor...
Either Alice or Betty will be elected	A ∨ B
Neither Alice nor Betty will be elected	~(A ∨ B) or (~A) ∧ (~B)

Both
Alice and Betty will not both be elected.	~(A ∧ B)
Alice and Betty will both not be elected.	(~A) ∧ (~B)

unless
Our resources will soon be exhausted unless more recycling of materials is effected	Either more recycling of materials is effected or our resources will soon be exhausted (M ∨ E)
Unless more recycling of materials is effected our resources will soon be exhausted

 

Exercises

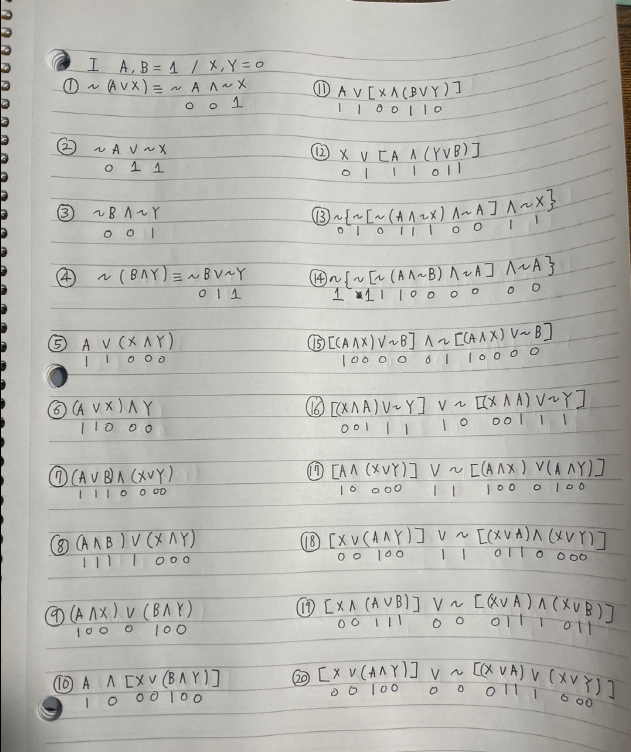
1. Since X is false, P ∧ X is also false.
2. Since B is true, B ∨ Q is also true.
3. Since ~A is false, ~A ∧ P is also false.
4. true 
5. Since ~Y is true, P ∨ ~Y is also true.
6. false 
7-9. true 
10. Q ∨ ~(P ∧ Q) ≡ Q ∨ (~P ∨ ~Q), true 
11. (P ∧ Q) ∨ (~Q ∨ ~P) ≡ (P ∧ Q) ∨ ~(P ∧ Q), true
12. (P ∨ Q) ∨ (~P ∧ ~Q) ≡ (P ∨ Q) ∨ ~(P ∨ Q), true 
13. Since ~B ∨ Y is false, (P ∨ Q) ∧ (~B ∨ Y) is also false.
14. true 
15. Since ~A ∨ X is false, (P ∨ Q) ∧ (~A ∨ X) is also false.
16-17. true  
18-19. false 
20. true

1. (A ∧ B) ∨ C
2. A ∧ (B  ∨ ~D)
3. ~(A ∧ B) ∧ (~C ∧ ~D)
4. (A ∨ B) ∧ ~(C ∨ D)
5. (C ∨ D) ∧ ~(C ∧ D)^[각주:5]
6. C ∨ A
7. ~~(A ∨ B)
8. ~C ∨ ~D
9. (C ∨ D)  ∧ (A ∧ B)
10. (C ∧ ~D)  ∨ (A ∧ B)

1. I will use '∧' instead of '•' for convenience. [본문으로]
2. (...) [본문으로]
3. [...] [본문으로]
4. {...} [본문으로]
5. exclusive disjunction [본문으로]