Frege and Russell's Paradox

2024-2 Frege and Russell Midterm Exam

#3)

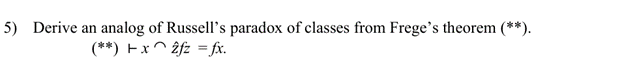
(A) It is widely known that Russell’s paradox of classes had fatal consequences for naive set theory. Suppose {z: z ∉ z}, i.e., the set of all objects that are not members of themselves, exists. We then immediately encounter a contradiction, as follows:

Call this set A, and ask “is A a member of itself?” If A ∉ A, then A meets the entrance requirement for A, whereupon A ∈ A. But on the other hand, if A ∈ A, then A fails to meet the entrance requirement and so A ∉ A. Thus both “A ∈ A” and “A ∉ A” are untenable (Enderton 1977: 6).

From this idea, we can formalize Rusell’s paradox as follows:

Russell’s Paradox “If R = {z: z ∉ z} exists, then R ∈ R iff R ∉ R, which is a contradiction” (Zach 2019: 13).

Here, “R ∈ R iff R ∉ R” is equivalent to

Let me move on to Frege’s trouble with Russell’s paradox. One of Frege’s central claims in his philosophy of mathematics is that numbers are purely logical objects (FA: 67). This thesis depends fundamentally upon his notion of correlation. According to Landini, “correlation gave Frege’s natural numbers a privileged status among set theoretical objects that all could play the role of natural numbers within set-theory” (Landini 2011: 93). As is well-known, Frege derived the following theorem from the definition of u ^ v and Basic Law V:

This is called the theorem of function correlation (Landini 2012: 87). Here, if the function fξ is a concept, i.e., its range exclusively includes the truth-values (the True and the False), then z´fz is its ‘concept correlate’ (Landini 2012: 87).

It is, however, misguided to translate the theorem into modern languages as follows:

For (**) expresses an identity relation rather than a biconditional one. Plus, fz must be understood as a functional term, not a formula (Landini 2012: 5). However, this does not mean that Frege’s original theorem (**) is immune to Russell’s paradox. We can derive an analog of Russell’s paradox of classes from Frege’s theorem (**) in the following way:

Recall that (**) is a schema.

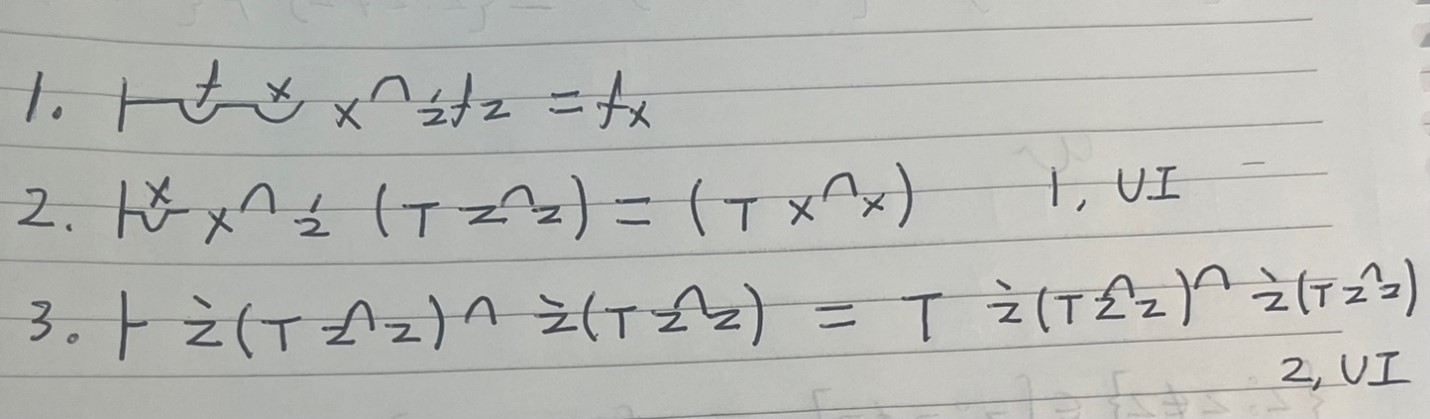
Clearly, we now arrived at a contradiction, i.e., ├ (―α) = (┬ α). Therefore, Russell’s paradox invalidates Frege’s original theorem (**) as well.

 

References

Dummett, Michael (1973). Frege: Philosophy of Language. London: Duckworth.

Enderton, Herbert (1977). Elements of Set Theory. New York: Academic Press.

Frege, Gottlob (FA). The Foundations of Arithmetic. A Logico-Mathematical Enquiry into the Concept of Number. translated by J. L. Austin. New York: Harper Torchbooks, 1960.

Frege, Gottlob (BLA). The Basic Laws of Arithmetic. Exposition of the System. translated and edited by Montgomery Furth, Berkeley and Los Angeles: University of California Press, 1967.

Frege, Gottlob (1891). “Function and Concepts.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.

Frege, Gottlob (1892a). “On Sinn and Bedeutung.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.

Frege, Gottlob (1892b). “On Concept and Object.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.

Hunter, Geoffrey (1971). Metalogic: an introduction to the metatheory of standard first order logic. Berkeley, CA: University of California Press.

Klement, Kevin C. (2001). Frege and the Logic of Sense and Reference. New York: Routledge.

Landini, Gregory (2011). Russell. New York: Routledge.

Landini, Gregory (2012). Frege’s Notations: What They Are and How They Mean. London and Basingstoke: Palgrave-Macmillan.

Landini, Gregory (2022) “Stipulations Missing Axioms in Frege’s Grundgesetze der Arithmetik,” History and Philosophy of Logic, 43:4, 347-382.

Zach, Richard (2019). Sets, Logic, Computation: An Open Introduction to Metalogic. Open Logic Project.