양상 연산자(Modal operator) L(□)과 M(◇)의 중요한 특징 중 하나는 그것들이 '모든(∀)'과 '어떤(∃)'의 개념을 포함하고 있다는 점이다. 즉, (세계 w에서 성립하는) 명제 Lp는 w가 볼 수 있는 모든 세계에서 p가 성립함을 뜻한다는 점에서 '모든'의 개념을 포함한다. 마찬가지로, Mp는 w가 볼 수 있는 어떤(최소한 하나 이상의) 세계에서 p가 성립함을 의미한다는 점에서 '어떤'의 개념을 포함한다. 따라서 우리는 양상 연산자가 쓰인 모든 문장을 양화 이론(quantification theory)으로 번역할 수 있다.
① (Lp)ʷ와 (Mp)ʷ
우선 Lp와 Mp에 대한 정의는 다음과 같다:

여기에서 (Lp)ʷ가 의미하는 바는 w가 볼 수 있는 모든 세계 α에서 p가 성립한다는 것이다 (명제 위의 첨자는 그 명제가 성립하는 세계를 지시한다) .
위 첨자의 사용으로 인해 초래될 수 있는 애매성을 방지하기 위해 우리는 아래의 네 가지 정의를 추가로 도입한다.
1. (p ⊃ q)ʷ =df pʷ ⊃ qʷ
2. (p ∨ q)ʷ =df pʷ ∨ qʷ
3. (p ∧ q)ʷ =df pʷ ∧ qʷ
4. (~p)ʷ =df ~(pʷ)
이제 L을 원초 기호(primitive symbol)로 정의하고, 이로부터 M을 정의한다고 가정해보자(물론 그 역도 가능하다). 먼저, 위에 제시된 바와 같이 Lp를 정의한다.
(Lp)ʷ =df (∀α)(wRα ⊃ pᵃ)
그런데 Mp ≡ ~L~p이므로,
(Mp)ʷ ≡ ~(∀α)(wRα ⊃ ~pᵃ)
또한 ~(∀x)는 (∃x)~이므로,
(Mp)ʷ ≡ (∃α)~(wRα ⊃ ~pᵃ)
Def ⊃에 따라,
(Mp)ʷ ≡ (∃α)~(~wRα ∨ ~pᵃ)
드모르간의 법칙(DeM)으로 괄호를 풀면,
(Mp)ʷ ≡ (∃α)(~~wRα ∧ ~~pᵃ)
이중부정(DN)을 적용하면,
(Mp)ʷ ≡ (∃α)(wRα ∧ pᵃ)
따라서 (Mp)ʷ는 (∃α)(wRα ∧ Pᵃ)로 정의되며 이것이 의미하는 바는 w가 볼 수 있는 어떤 (최소한 하나 이상의) 세계가 있고 바로 이 세계에서 p가 성립한다는 것이다.
② Axiom K: L(p ⊃ q) ⊃ (Lp ⊃ Lq)
System K의 기본 공리 L(p ⊃ q) ⊃ (Lp ⊃ Lq)는 모든 frame에서 타당하다.
먼저 L(p ⊃ q) ⊃ (Lp ⊃ Lq)가 거짓이라고 가정하자. 이 경우 L(p ⊃ q)와 Lp는 참이고 Lq는 거짓이다.
~Lq
L-M Interchange(LMI)에 따라,
~~M~q
이중부정(DN)을 적용하면,
M~q
즉, L(p ⊃ q), Lp, 그리고 M~q는 모두 w에서 참이다.
w₁: L(p ⊃ q), Lp, M~q
↓
w₂: p ⊃ q, p , ~q ▶ p, q, ~q
요컨대 (q ∧ ~q)ʷ²이므로 모순이 도출된다. 따라서 우리는 특정한 frame을 가정하지 않고도 다음과 같이 간단하게 K를 증명할 수 있다.
⊦ (∀α)(wRα ⊃ (p ⊃q)ᵃ) .⊃. (∀α)(wRα ⊃ pᵃ) ⊃ (∀α)(wRα ⊃ qᵃ)

③ Axiom D: Lp ⊃ Mp
System D의 기본 공리 Lp ⊃ Mp는 serial frame에서 성립한다. 즉,
Serial (R) =df (∀w)(∃u)(wRu)
이는 어떤 Model이든지 간에 w가 최소한 하나 이상의 세계를 볼 수 있어야 함을 의미한다. w가 볼 수 있는 세계가 (자기자신을 포함하여) 단 하나도 존재하지 않을 때, 그러한 세계를 dead end라고 부른다. dead end에서 Mp는 항상 거짓이다. 왜냐하면, (∃α)(wRα ∧ Pᵃ)에서 wRα와 Pᵃ의 연언은 (wRα가 거짓이므로) 항상 거짓이 되기 때문이다. 반대로, dead end에서 Lp는 항상 참이다. 왜냐하면, 전건 wRα가 거짓이므로 wRα ⊃ Pᵃ 전체는 언제나 사소하게(trivially) 참이 되기 때문이다. 따라서 dead end에서는 M(p ⊃ p)마저 거짓이며, L(p ∧ ~p) 마저 참이다.
이제 Lp ⊃ Mp가 거짓이라고 가정하자.
~(Lp ⊃ Mp)
Def ⊃에 따라,
~(~Lp ∨ Mp)
드모르간의 법칙(DeM)으로 괄호를 풀면,
~~Lp ∧ ~Mp
이중부정(DN)을 적용하면,
Lp ∧ ~Mp
위에서 확인한 바와 같이, Dead end에서는 (Lp ∧ ~Mp)가 참이므로 D가 거짓이어도 모순이 도출되지 않는다. 즉, 이러한 세계를 포함하고 있는 frame에서 D는 타당하지 않다.
반면, serial frame 하에서는 다음이 성립한다.
w₁: Lp, ~Mp
↓
w₂: p, ~p
요컨대 (p ∧ ~p)ʷ²이므로 모순이 도출된다.
또한 당연하게도, reflexive, transitive, 그리고 symmetric frame은 모두 serial frame을 함축한다. 즉, Lp ⊃ Mp는 T, S4, B, S5의 정리이다.
⊦ (∀α)(wRα ⊃ pᵃ) ⊃ (∃α)(wRα ∧ pᵃ)

④ Axiom T: Lp ⊃ p
System T의 기본 공리 Lp ⊃ p는 reflexive frame에서 성립한다. 즉,
Refl (R) =df (∀w)(wRw)
이는 어떤 Model이든지 간에 w가 최소한 자기자신을 볼 수 있어야 함을 의미한다. 왜 이러한 조건이 필요한가? 만약 w가 자기자신을 볼 수 없다면, (∀α)(wRα ⊃ Pᵃ) ∧ ~(p)ʷ인 세계는 명백하게도 허용 가능하다. 그런데 (Lp ∧ ~p) ≡ ~(Lp ⊃ p)이므로, 이러한 세계에서는 T가 거짓이어도 모순이 도출되지 않는다. 즉, 이러한 세계를 포함하고 있는 frame에서 T는 타당하지 않다.
반면, reflexive frame 하에서는 다음이 성립한다.
w: Lp, ~p, p
요컨대 (p ∧ ~p)ʷ이므로 모순이 도출된다.
⊦ (∀α)(wRα ⊃ pᵃ) ⊃ pʷ

⑤ Axiom S4: Lp ⊃ LLp
System S4의 기본 공리 Lp ⊃ LLp는 transitive frame에서 성립한다. 즉,
Trans (R) =df (∀w)(∀α)(∀β)(wRα ∧ αRβ .⊃. wRβ)
이는 어떤 Model이든지 간에 w가 α를 볼 수 있고, α가 β를 볼 수 있다면, w 또한 β를 볼 수 있어야 함을 의미한다. 왜 이러한 조건이 필요한가? 우선 Lp ⊃ LLp가 거짓이라고 가정하자. 이 경우 Lp는 참이고, LLp는 거짓이므로, Lp와 MM~p는 w에서 모두 참이다(~LLp ≡ MM~p). 여기에서 만약 w가 transitive frame이 아닐 경우 다음이 성립한다:
w₁: Lp, MM~p
↓
w₂: p, M~p
↓
w₃: ~p
이 경우 모순이 도출되지 않는다. 즉, 이러한 세계를 포함하고 있는 frame에서 S4는 타당하지 않다.
반면, transitive frame 하에서는 다음이 성립한다.
w₁: Lp, MM~p
↓ ↘
w₂: p, M~p
↓ ↙
w₃: ~p, p
요컨대 (p ∧ ~p)ʷ³이므로 모순이 도출된다.
⊦ (∀α)(wRα ⊃ pᵃ) ⊃ (∀α)(wRα ⊃ (∀β)(αRβ ⊃ pᵝ))
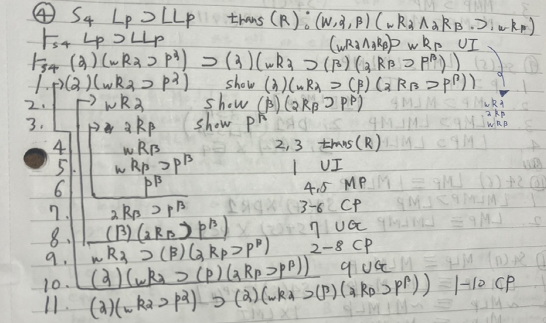
⑥ Axiom B: p ⊃ LMp
System B의 기본 공리 p ⊃ LMp는 symmetric frame에서 성립한다. 즉,
Symm (R) =df (∀w)(∀α)(wRα ⊃ αRw)
이는 어떤 Model이든지 간에 w가 α를 볼 수 있다면 α 역시 w를 볼 수 있어야 함을 의미한다. 왜 이러한 조건이 필요한가? p ⊃ LMp가 거짓이라고 가정하자. p는 참이고, LMp는 거짓이므로, p와 ML~p는 w에서 모두 참이다(~LMp ≡ ML~p). 여기에서 만약 w가 symmetric frame이 아닐 경우 다음이 성립한다:
w₁: p, ML~p
↓
w₂: L~p
↓
w₃: ~p
이 경우 모순이 도출되지 않는다. 즉, 이러한 세계를 포함하고 있는 frame에서 B는 타당하지 않다. 반면 symmetric frame 하에서는 다음이 성립한다.
w₁: p, ML~p, ~p
↓ ↑
w₂: L~p
즉, 우리는 w₂의 L~p로부터 w₁에 ~p를 가져올 수 있다. 이 경우 (p ∧ ~p)ʷ¹이므로 모순이 도출된다.
⊦ pʷ ⊃ (∀α)(wRα ⊃ (∃β)(αRβ ∧ pᵝ))

⑦ Axiom S5: Mp ⊃ LMp
System S5의 기본 공리 Mp ⊃ LMp는 transitive & symmetric frame에서 성립한다.
Mp ⊃ LMp가 거짓이라고 가정하자. 이 경우 전건 Mp는 참이고 후건 LMp는 거짓이다. 따라서 Mp와 ML~p는 w에서 모두 참이다(~LMp ≡ ML~p). 여기에서 만약 w가 transitive & symmetric frame이 아닐 경우 다음이 성립한다:
w₁: Mp, ML~p
↓ ↘
w₂: L~p w₃: p
↓
w₄: ~p
이 경우 모순이 도출되지 않는다. 즉, 이러한 세계를 포함하고 있는 frame에서 S5는 타당하지 않다. 반면 transitive & symmetric frame 하에서 w₂는 symm(R)에 따라 w₁을 볼 수 있고, trans(R)에 따라 (w₂Rw₁ ∧ w₁Rw₃ .⊃. w₂Rw₃ 이므로) w₃ 또한 볼 수 있다. 즉,
w₁: Mp, ML~p
↓ ↘
w₂: L~p → w₃: p, ~p
↓
w₄: ~p
이 경우 (p ∧ ~p)ʷ³이므로 모순이 도출된다.
⊦ (∃β)(wRβ ∧ pᵝ) ⊃ (∀α)(wRα ⊃ (∃β)(αRβ ∧ pᵝ))

'Logic > Modal Logic' 카테고리의 다른 글
| The Tableau Method (1) Normal Modal Logic (0) | 2024.01.04 |
|---|---|
| Translation into quantification theory (2) (0) | 2024.01.04 |
| Chapter 3. The Brouwerian System (0) | 2024.01.04 |
| Chapter 3. The System S5 (0) | 2024.01.04 |
| Chapter 3. The System S4 (0) | 2024.01.03 |