G.E. Hughes & M.J. Cresswell, A New Introduction to Modal Logic, London and New York: Routledge, 1996, pp. 58-62.
(5) The System S5
① S5 Mp ⊃ LMP
S5 (or E) Mp ⊃ LMP [R1a]
② Translation into quantification theory

③ S5 (1)-(3)


④ S4 Lp ⊃ LLp (as a theorem of S5)

⑤ S5 (4)-(7)

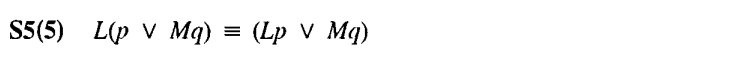
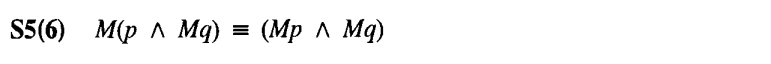
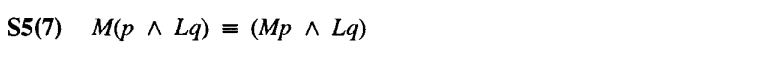


⑥ S5* (MLp ∧ Mq) ⊃ M(p ∧ q)

⑦ S5 is not a theorem of S4

∴ S5 properly contains S4
(6) Modalities in S5

① In any pair of adjacent modal operators we may delete the first.
② Since this procedure may be repeated indefinitely, we have the more comprehensive rule that in any sequence of modal operators we may (in S5) delete all but the last.
③ S5 contains at most six distinct modalities, viz.

(7) Validity for S5
① symm (R)
A frame <W, R> is symmertical iff for any w and w' in W, if wRw' then w'Rw.
② Tableau

③ A relation which is reflexive, transitive and symmetrical is known as an equivalence relation (S5-frame)
④ SS-validity
- (a) An everyday example of an equivalence relation is ‘has the same height as’, and this can be used to illustrate the fact that when such a relation is defined over a class of objects it divides them into a number (though perhaps only one) of self-contained ‘equivalence classes’.
- (b) Thus if ‘has the same height as’ is defined over a class of human beings, then for each height that any of them has there will be the ‘equivalence class’ of all and only those who have that height.
- (c) Within each such equivalence class everyone will have the relevant relation to everyone, but no one will have that relation to anyone in any other equivalence class.
- (d) To apply this to frames: if in a frame (W,R) R is an equivalence relation, this means that every world will be able to see every world in its own equivalence class but no world in any other equivalence class, and hence that we can equally well think of such a frame, not so much as a single frame but as a collection of separate frames, in each of which every world can see every world.
- (e) we could equally well, and equivalently, define SS-validity as validity on every frame in which R is a universal relation, i.e. one which holds between every pair (distinct or identical) of worlds in that frame.

⑤ The validity of some S5 theorems

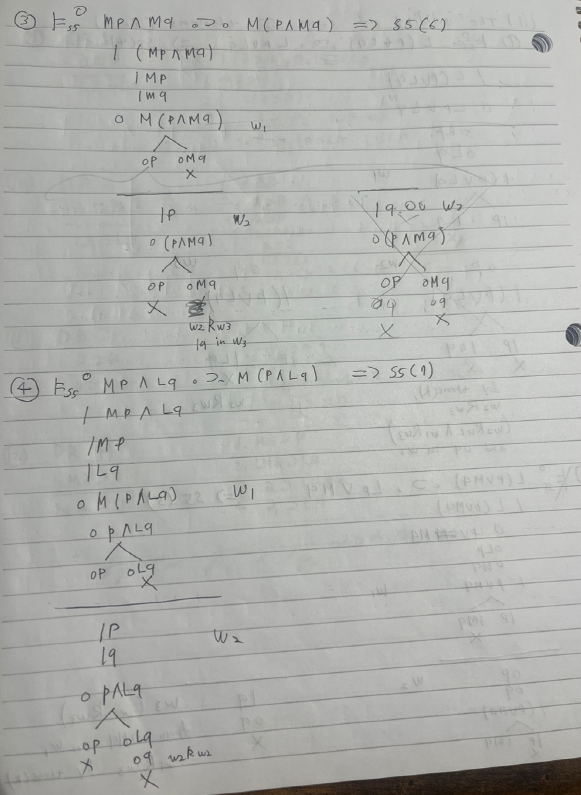
'Logic > Modal Logic' 카테고리의 다른 글
| Translation into quantification theory (1) (0) | 2024.01.04 |
|---|---|
| Chapter 3. The Brouwerian System (0) | 2024.01.04 |
| Chapter 3. The System S4 (0) | 2024.01.03 |
| Chapter 3. Iterated Modalities (0) | 2024.01.03 |
| Chapter 2. The System D (0) | 2024.01.03 |