2024-2 Frege and Russell

(A) One of the main differences between the Principles Era (1900-1908) and the Principia Era (1909-1917) is that only the former adopted the ontology of propositions while the latter abandoned it. In other words, there are no propositions in the Principia. This requires the meticulous and subtle reading of Russell’s works from the Principles Era, since the notation Russell developed is quite distinct from both the notation of Principia and our own.
For Russell, propositions are an esoteric notion that is not fit into our modern notation. To see this, let us consider the following wff:
ϕ ⊃ ψ
Without a doubt, both ϕ and ψ must be wffs (well-formed formulas) in our modern notation. Of course, the whole expression ϕ ⊃ ψ is also a wff. This becomes evident when we substitute it with its logical equivalent:
~ϕ ∨ ψ
Modern notation does not allow logical constants (e.g., ~, ∨) to be attached to terms. It would be nonsensical to say “not Socrates.” Only formulas can be combined with logical constants to form new formulas. However, in the Principles Era, both ϕ and ψ are terms, and only the entire expression ϕ ⊃ ψ is a wff.
For convenience, let us use Ɔ instead of ⊃. Then ϕ Ɔ ψ is not akin to our material implication but rather to a wff containing a relation sign, e.g., xLy (“x loves y”). Like ϕ Ɔ ψ, both x and y are terms in xLy, and only the entire expression is considered a wff. Given this, ϕ Ɔ ψ could be rewritten as:
Ɔ ϕ ψ
Or,
Ɔ (ϕ, ψ)
If we wanted to make a sharp contrast between it and our modern material implication sign.
Therefore, whereas ϕ ⊃ ψ is commonly interpreted as “if Fx, then Gy,” ϕ Ɔ ψ should not be read in the same way. One possible interpretation is to read it as “ϕ implies ψ.”
A problem remains. Since propositions are either true or false, Russell’s notation seems to be seriously flawed. How can we reconcile the common understanding of propositions with Russell’s peculiar notation? Let us consider the following proposition:
The cat is on the mat.
We can then nominalize this sentence as follows:
The cat’s being on the mat
The latter expression is now a term, not a formula. Therefore, [-] Ɔ [-] can be filled by such nominalized wffs. Now, let’s suppose ϕ is “the cat is on the mat” and ψ is “the dog is on the house.” Those wffs can be nominalized as follows:
{ϕ}: the cat’s being on the mat
{ψ}: the dog’s being on the house
Consequently, we can give the following proper interpretation:
{ϕ} Ɔ {ψ}: the cat’s being on the mat implies the dog’s being on the house.
Here, propositions are defined as the reference of nominalized wffs. Within Russellian notation, ϕ .⊃. ψ ⊃ ϕ would be:
{ϕ} Ɔ {{ψ} Ɔ {ϕ}}
, which can be read as “ϕ implies ψ’s implying ϕ.”
Let me now consider the rule of Modus Ponens. According to our modern notation, Modus Ponens is as follows:
From ϕ and ϕ ⊃ ψ, infer ψ
Or,
ϕ, ϕ ⊃ ψ ├ ψ
In Russellian notation, it would be:
ϕ, {ϕ} Ɔ {ψ} ├ ψ
This can be called PoM Modus Ponens. Likewise, let me consider the rule of simplification. In modern notation, simplification is as follows:
From ϕ ∧ ψ, infer ψ
Or,
ϕ ∧ ψ ├ ψ
In Russellian notation, it would be:
{ϕ} ∧ {ψ} ├ ψ
This can be called PoM Simplification. One might ask about the meaning of conjunction in Russell’s notation. Given that ϕ ∧ ψ is defined as ~(ϕ ⊃ ~ψ) in our notation1, {ϕ} ∧ {ψ} is defined as ~({ϕ} Ɔ ~{ψ}). Here, the negation sign is defined as follows:
~x =df x Ɔ f
, where f is “the False.” Thus, the Russellian conjunction now can be defined as:
x ∧ y =df (x Ɔ (y Ɔ f)) Ɔ f
And the False is defined as:
f =df (∀x)(∀y)(x Ɔ y)
In 1905, Russell developed his “no-classes” theory to resolve the paradoxes that the Fregean logicism program encountered (Landini 1998: 97). Since it was intended to serve as a proxy for a type regimented theory by using type-free calculus, it is also called “the substitutional theory” (Landini 1998: 97). To understand this theory, let us first consider Russell’s simple type theory. In his simple type theory, all the variables are individual variables, i.e., x, y, z, u, v, w and so on. For the lowest type, we can place a small zero on each individual variable as follows:
x0, y0, z0
The zero and brackets indicate the next higher type:
x(0), y(0), z(0)
And the proper interpretation of x(0), y(0), z(0) is that they are properties of individuals, i.e., x0, y0, z0. Moreover, we can designate the second-order type as follows:
x((0)), y((0)), z((0))
And then the interpretation of x((0)), y((0)), z((0)) is that they are properties of properties of individuals, x0, y0, z0.
Now, note that all those signs are terms, not formulars. How do they look like in wffs? It could be like this:
x(0)(x0)
Here, to become a formula the matching requirement is needed. The matching requirement is that one simple type symbol has to match another in a formula. The violation of the matching requirement makes a formular ungrammatical. x((0))(x0), for instance, is an ill-formed formula in Russell’s notation. If the type is relational, we could describe it by using two arguments such as y(0, 0)(x0, z0).
The essence of his substitutional theory is to substitute an entity2 for another in a given proposition, allowing definite descriptions of propositions (Landini 1998: 97). Russell first introduced the notion of substitution as follows:
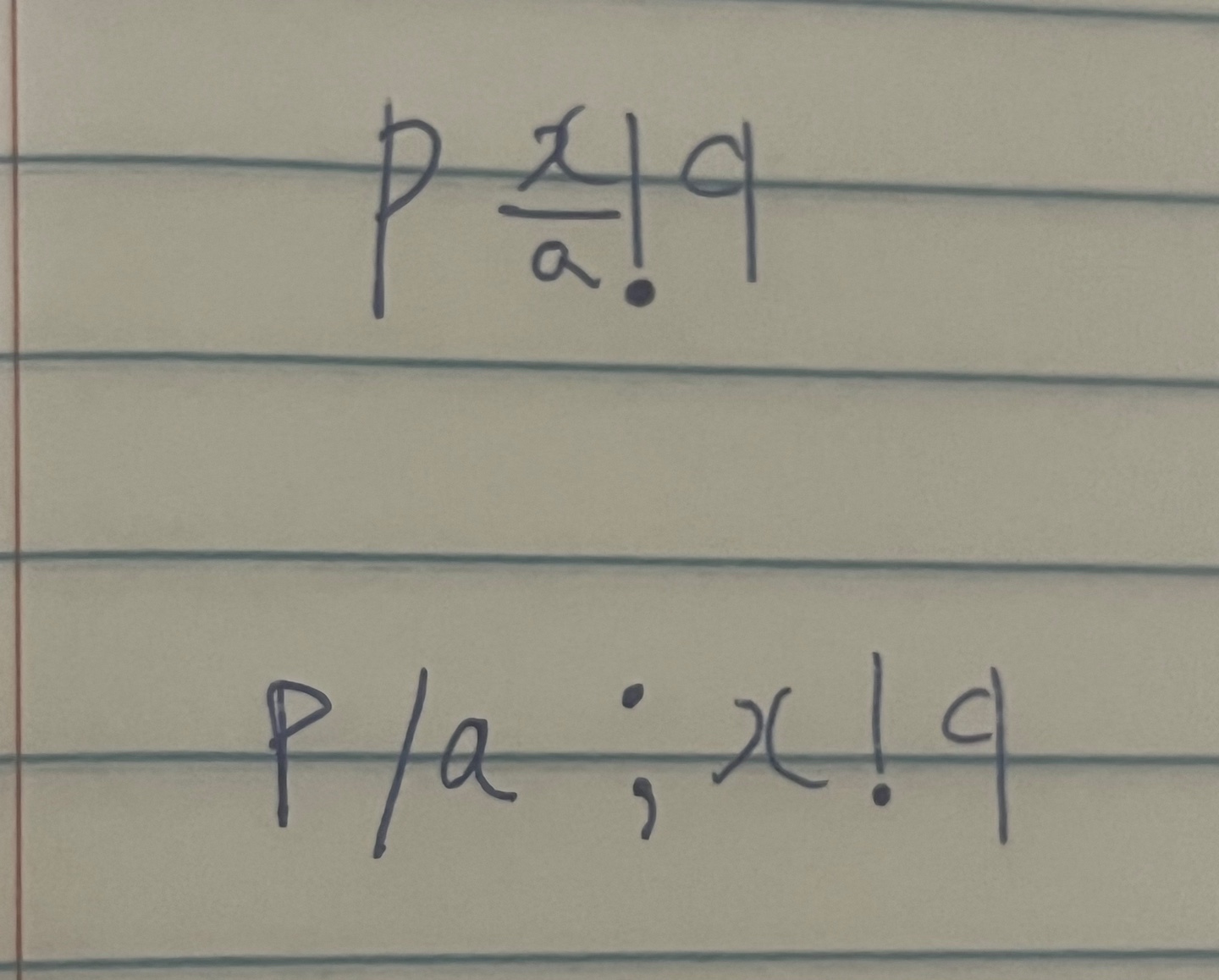
It means that “q results from p by substituting x for a in all those places (if any) where a occurs in p” (Landini 1998: 98). Russell also incorporated his theory of descriptions into the substitutional theory. Within this framework, he introduced the novel expression, p/a;b, as follows:
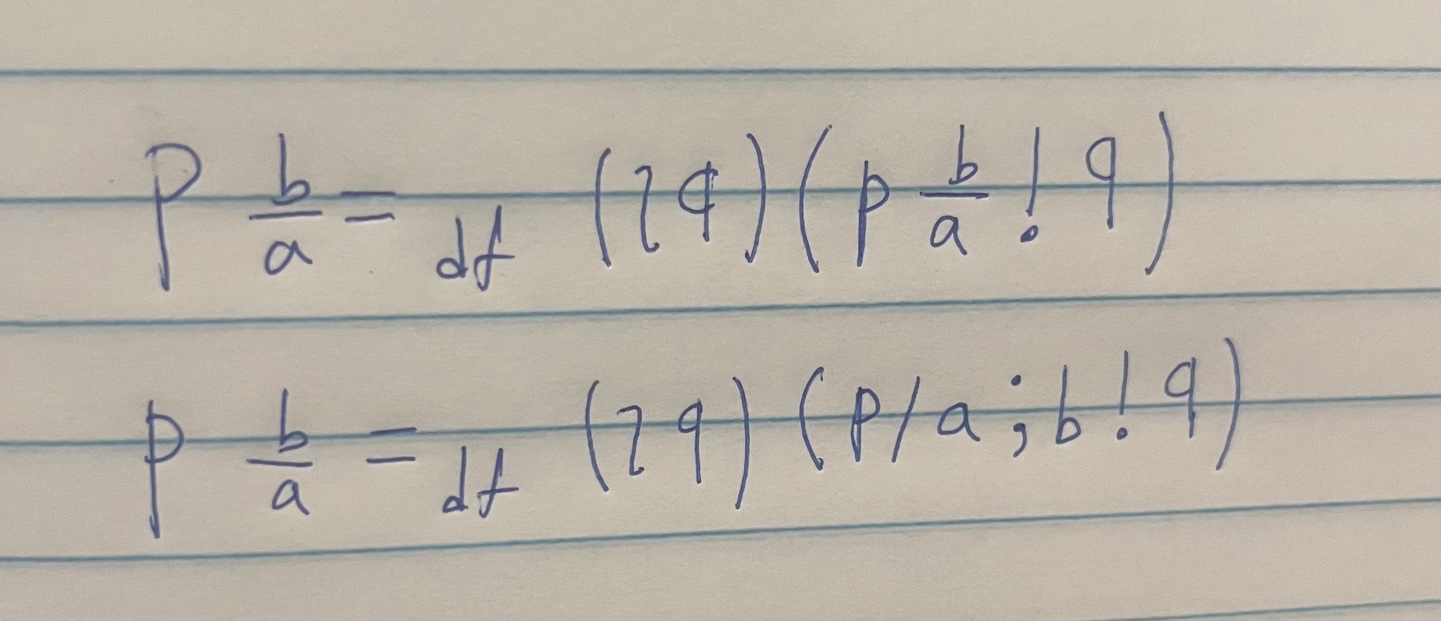
p/a;b is a definite description of an entity q which is structurally exactly like p except for containing b wherever p contains a (Landini 1998: 129). In other words, q is an entity resulting from the substitution of a contained in p with b, without exception.
By using this notation, we can now translate wffs of the language of simple type theory into the language of substitutional theory, i.e., substitution in lowest simple type. For example, let’s take the following wff:

We could emulate simple types by using a number of variables. Since the wff contains the second-order type ((0)), we need three variables such as (∃s, t, w). Likewise, we need two variables, such as (p, a), for (0). Then there is q, which is the outcome of the substitution of t with p and w with a. Both t and w were contained in s, and q is exactly like s except for containing p and a where s contains t and w. As a result, we arrive at the following translation:

Or, by using the definite descriptions,

Next, let us consider the following wff:

We can translate this as follows:

, where p/a = p/a is defined as p = p ∧ a = a.
Finally, let us take the Russell’s famous example of the great general (Landini 2007:153-154). We have:
(∃ϕ)(x)(ϕ!x ≡ (ψ)( (z)(Great general (z) ⊃ ψ!z) .⊃. ψ!x) ).
By designating zero and brackets, we get:

The translation is as follows:

All the translations clearly show that the role of substitution is to eliminate every higher type while resulting in a substitute that is structurally exactly like an original entity. In other words, through the substitutional theory, we can obtain simple type-free formulas and yet emulate simple types of properties and relations.
Another strength of the substitutional theory is that we can avoid Russell’s paradox of properties, i.e., (∃ϕ)(x)(ϕ!x ≡ (∃Γ)( x= Γ! .&. ∼Γ!x)), in the language of substitutional theory. In fact, we cannot even write it down in this language since the expression like ϕ(ϕ) cannot be proxied in the substitutional grammar (Landini 1998: 143). To express this, we would need

which is ungrammatical.
References
Irvine, Andrew David (2024). “Bertrand Russell,” The Stanford Encyclopedia of Philosophy (Winter 2024 Edition), Edward N. Zalta & Uri Nodelman (eds.), URL = <https://plato.stanford.edu/archives/win2024/entries/russell/>.
Kant, Immanuel (1998). Critique of Pure Reason. Translated by Paul Guyer and Allen W. Wood. Cambridge: Cambridge University Press.
Kant, Immanuel (1998). Groundwork of the Metaphysics of Morals. Translated and edited by Mary Gregor. Cambridge: Cambridge University Press.
Landini, Gregory (1998). Russell’s Hidden Substitutional Theory, Oxford: Oxford University Press.
Landini, Gregory (2007). Wittgenstein’s Apprenticeship with Russell, Cambridge: Cambridge University Press.
Landini, Gregory (2011). Russell. New York: Routledge.
Landini, Gregory (2021). Repairing Bertrand Russell’s 1913 Theory of Knowledge. London and Basingstoke: Palgrave-Macmillan.
Monk, Ray (1991). Ludwig Wittgenstein: The Duty of Genius. New York: Vintage.
Russell, Bertrand (1959). “The Relation of Sense-Data to Physics.” In: Mysticism and Logic and Other Essays. London: George Allen & Unwin LTD.
Russell, Bertrand (2001). The Problems of Philosophy. Oxford: Oxford University Press.
Russell, Bertrand (2009). Our Knowledge of the External World As a field for scientific method in philosophy. London and New York: Routledge.
Soames, Scott (2014). The Analytic Tradition in Philosophy. Vol. 1 The Founding Giants. Princeton and Oxford: Princeton University Press.
Wittgenstein, Ludwig (1921). Tractatus Logico-Philosophicus. Translated by Pears and McGuinness. New York: Routledge.
-
Proof:
1. ~(ϕ ⊃ ~ψ) ≡ ~(~ϕ ∨ ~ψ), by Def ⊃
2. ~(~ϕ ∨ ~ψ) ≡ ~~ ϕ ∧ ~~ ψ, by DeM
3. ~~ ϕ ∧ ~~ ψ ≡ ϕ ∧ ψ, by DN
- Landini (1998) argued that “Russell's ‘substitution’ concerns entities not symbols. Substitution is ontological, not linguistic” (98). Given this, the word ‘substitution’ might be misleading because we could easily associate this notion with the replacement of linguistic symbols in other linguistic symbols in which our manipulation is involved (Landini 1998: 98). [본문으로]
'Logic > Phil of Logic' 카테고리의 다른 글
| 전기 비트겐슈타인의 근본 사상과 논리의 본성 (0) | 2024.11.08 |
|---|---|
| Fregean Concepts (0) | 2024.10.30 |
| On the Tractarian Concept of 'senseless (sinnlos)' (0) | 2024.02.28 |
| 초월 논리의 또 다른 길 -칸트, 프레게, 그리고 비트겐슈타인- (0) | 2023.12.06 |