G.E. Hughes & M.J. Cresswell, A New Introduction to Modal Logic, London and New York: Routledge, 1996, pp. 24-33.
(2) The System K
① The system K is one which will turn out to have as its theorems precisely those modal formulae which are K-valid.
② The axioms of the system K consist of
- (a) all valid wff of PC
- (b) the single distinctively modal wff, K
PC: If α is a valid wff of PC, then α is an axiom
K: L(p ⊃ q) ⊃ (Lp ⊃ Lq)
③ Notation

④ Three primitive (i.e., initially given) transformation rules


※ US and MP are not specifically modal rules. US in particular is a rule that it is plausible to require of any logical system with a class of symbols to be interpreted as propositional variables.
※※ MP simply reflects the truth-functional meaning of ⊃
※※※ N, which is a specifically modal rule, also preserves K-validity, for this reason: Suppose α is K-valid - i.e. in every setting every player would raise a hand for α; then every player that any player can see would raise a hand for α; so by the rule for L, every player would raise a hand for Lα- i.e. Lα is K-valid.
⑤ Translation into quantification theory

(3) Proofs of theorems
① A proof of a theorem α in a system S consist of a finite sequence of wff, each of which is either
- (a) an axiom of S or,
- (b) a wff derived from one or more wff occurring earlier in the sequence, (b-1) by one of the transformation rules or (b-2) by applying a definition, α itself being the last wff in the sequence.
② The proof of K1
K1 L(p ∧ q) ⊃ (Lp ∧ Lq)

③ The proof of K2
K2 (Lp ∧ Lq) ⊃ L(p ∧ q)

④ K1 and K2
K2 is the converse of K1
K1(L(p ∧ q) ⊃ (Lp ∧ Lq)) + K2((Lp ∧ Lq) ⊃ L(p ∧ q)) = K3
⑤ The proof of K3 (Laws of L-distribution)

⑥ Drived rule of K (PC5)
we can use PC51 in this way not only in the case of K1 and K2, but whenever we have already proved both a wff of the form α ⊃ β and its converse β ⊃ α; i.e. by substituting α for p and β for q in PC5 and applying MP twice, we can obtain α ≡ β.

(This rule is not part of the axiomatic basis of K. Nevertheless it is what we call a derived rule of K, in the sense that we may always use it as a transformation rule in a proof, since anything we can prove by using it we could also prove, though at greater length, from the axiomatic basis alone.)
To establish that a rule is a drived rule of a system we may simply show how we could always do without it.

The procedure we have described for the use of PC5 will in fact enable us to derive a rule of K from any valid PC wff whose main operator is ⊃. For if α is a valid PC wff, it is an axiom of K, and hence, by US, all its substitution-instances are theorems of K. So if α is a valid PC wff, it is an axiom of K. So if we can make substitutions for the variables in α which will turn it into a wff whose antecedent is a wff we have already proved, we can use MP to detach its consequent and count that as a theorem too. (This is why MP is sometimes called Detachment.)
⑦ Drived rule (Syll)
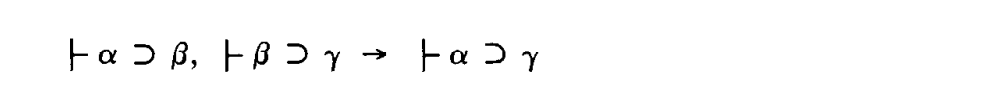

⑧ Derived Rule 1


⑨ The proof of K1-K3 in the abbreviated style
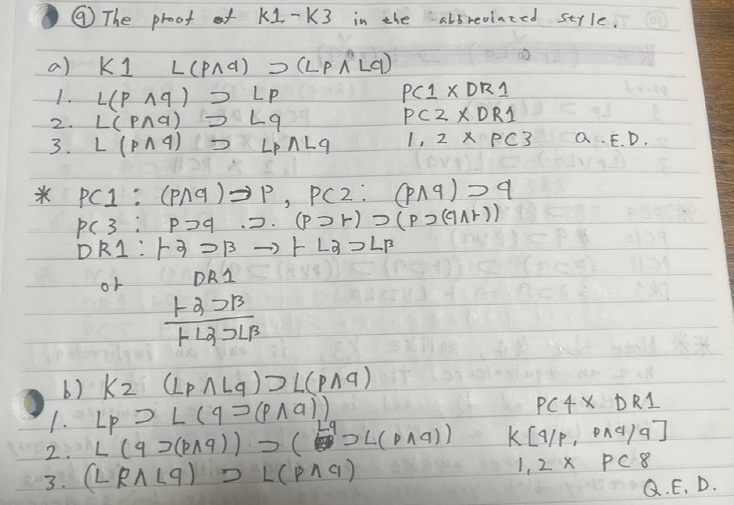

⑩ The proof of K4


※ Note that K4, unlike K3, is only an implication, not an equivalence. The converse of K4 is not a theorem of K, and in fact at the intuitive level is not a valid formula: it may be necessary that you are awake or asleep without its being necessary that you are awake or its being necessary that you are asleep.
⑪ Derived Rule 2
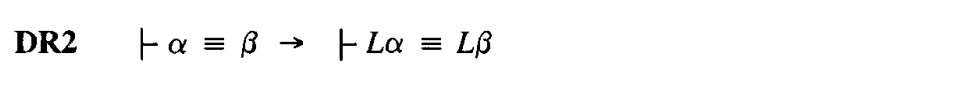

⑫ Derived Rule (Substitution of Equivalents) ≒ Eq
- (a) if α is a theorem and β differs from α only in having some wff, δ, at one or more places where α has a wff, γ, then if y = δ is a theorem, β is a theorem.
- (b) if we have proved γ ≡ δ, we can replace γ by δ in any theorem (not necessarily uniformly), and the result will also be a theorem.
- (c) some valid wff of PC (which are at the same time axioms of K)

- (d) proof

- (e) if α is any wff which is built up from γ using ~ and L as the only monadic operators and ∨ as the only dyadic one, and β is built up from δ in exactly the same way as α is from γ, then if γ ≡ δ is a theorem, so is α ≡ β.
- (f) and therefore, if α is a theorem, then by MP so is β.
- (g) Since every modal wff can be written with ~, L and ∨ as its only operators, what we have just shown is that we can apply Eq unrestrictedly in K; i.e. whenever we have a theorem of K of the form γ ≡ δ, we can replace γ by δ in any theorem α, no matter where γ occurs in α, and the result will also be a theorem of K.
- (h) Where an equivalential wff has a name, e.g. K3, and we are using Eq to replace an instance of one side of the equivalence by an instance of the other side in some wff, we shall indicate the application of Eq by (in this example) ‘ X K3 X Eq’, and analogously in other cases. A rich source of equivalential wff is of course provided by valid PC equivalences.
Appendix I: comparison (theorems)





Appendix II: comparison (DR)

- ((p ⊃ q) ⊃ (q ⊃ p)) ⊃ (p ≡ q) [본문으로]
'Logic > Modal Logic' 카테고리의 다른 글
| Chapter 2. The System T (0) | 2024.01.03 |
|---|---|
| Chapter 2. The System K (K5-K9, and K*) (0) | 2024.01.02 |
| Chapter 2. An Axiomatic Basis for a Logical System (0) | 2024.01.02 |
| Chapter 1. Basic Modal Notions (0) | 2024.01.02 |
| Chapter 1. The Language of PC (0) | 2023.12.31 |