G.E. Hughes & M.J. Cresswell, A New Introduction to Modal Logic, London and New York: Routledge, 1996, pp. 3-13.
(1) The Language of PC (Propositional Carculus)
① Primitive (or undefined) symbols of PC
1. A set of letters: p, q, r, . . . (with or without numerical subscripts). We suppose ourselves to have an unlimited number of these.
2. The following four symbols: ~, V, (, ).
※ Any symbol in the above list, or any sequence of such symbols, we call an expression. An expression is either a formula - more exactly a well-formed formula (wff) - or else it is not. We are concerned only with expressions which are well-formed formulae (wff).
② The Formation Rules of PC
FR1 A letter standing alone is a wff.
FR2 If α is a wff, so is ~α.
FR3 If α and β are wff, so is (α ∨ β).
※ α, β = metalogical variables (used in talking about the system. They are not among the symbols of the system)
(2) Interpretation
① The letters = propositional variables = variables whose values are propositions.
② Proposition ≒ statement (what is stated), assertation (what is asserted)
Every proposition is either true or false, and no proposition is both true and false. (Hence if something is neither true nor false, or is capable of being both true and false, it is not to count as a proposition in the present context.).
③ Truth and falsity are said to be the truth-values of propositions.
④ Proposition-Forming Operators
1. ~ : (it is not the case that) p
2. ∨ : (either...or...)
3. Both ~ and ∨ are Proposition-Forming Operators on proposition
4. The propositions on which such an operator operates are called its arguments.
5. If an operator requires only a single argument (e.g., ~), it is said to be monadic. If it requires two (e.g., ∨), it is said to be dyadic.
6. Whenever we are given the truth-value of the argument or arguments, we can deduce the truth-value of the complex proposition.
7. The truth-value of a proposition formed by means of a truth-functional operator (e.g., ~, ∨) depends in every case only on the truth-value of the operator's argument or arguments.

⑤ The Interpretation of '~'
~ : not, negation sign
~p : the negation of p

⑥ The Interpretation of '∨'
∨ : or, disjunction sign
Its arguments are disjuncts
p ∨ q : the disjunction of p and q

⑦ All operators in ordinary (two-valued) PC are truth-functional and for this reason PC is sometimes called the theory of truth functions.
(3) Further Operators

When a wff contains no symbols except primitive ones it is said to be written in primitive notation. The definitions enable us to write all wff in primitive notation if we wish to do so.
(4) The Interpretation of ∧, ⊃, and ≡
ⓛ The Interpretation of ∧
∧ : and, conjunction sign.
A wff formed with ∧ is known as conjunction, and the arguments are called conjuncts.
The basic truth-table for ∧ :

② The Interpretation of ⊃
⊃ : 'if..., then...,' (materially implies)
(material) implication sign
The first argument: antecedent
The second argument: consequent
The basic truth-table for ⊃ :

③ The Interpretation of ≡
≡ : '...is (materially) equivalent to...,' 'if and only if'
(material) equivalence sign
A proposition formed with ≡ is true when both arguments have the same truth-value, false when they have different truth-values.
The basic truth-table for ≡ :

(5) Validity
① If we regard the variables, p, q, r, . . . as taking the whole range of propositions as their values, we can say that a wff of PC becomes a proposition when all its variables are replaced by propositions. A wff is said to be valid iff the result of every such replacement is a true proposition.
② If, however, we speak instead of the variables taking simply the two truth-values 1 and 0 as their values, we shall say that a wff is valid iff it always has the value 1, no matter what truth-values are (uniformly) assigned to its variables.
③ Simple examples of valid wff are p ∨ ~p and (p ∧ q) ⊃ p. A valid wff of PC is often called a tautology or a PC-tautology.
④ A wff is said to be unsatisfiable iff it always has the value 0, no matter what truth-values are (uniformly) assigned to its variables (e.g., p ∧ ~p).
⑤ Many wff, such as p ⊃ q, are of course neither valid nor unsatisfiable.
⑥ PC-game
- ⓐ We give a player a sheet of paper on which we have previously written a number of letters of the alphabet (preferably taken from the series, p, q, r, . . . etc.).
- ⓑ The player and the sheet are called as a setting of the PC game, or more succinctly a PC-setting.
- ⓒ We then call out to the player wff of PC, to which the player is to respond by either raising his or her hand or keeping it down.
- ⓓ Before a wff α is called we must have previously called all the formulae which occur as parts of α (so, if p ∧ ~p is to be called, we must first call p, and then ~p, and only then may we call p ∧ ~p)


- ⓔ If the player in a PC-setting raises his or her hand when a PC wff α is called, we shall say that α is successful in that setting.
- ⓕ Many formulae will be successful in some settings but not in others (depending of course on which letters appear on the sheet for a given setting). But there will be some formulae which will be successful in every PC- setting (e.g., p ∨ ~p). These we call PC-successful.
⑦ The PC-successful wff are precisely those which are PC-valid
- ⓐ Let us call the sheet of variables an assignment of truth-values with the idea that a variable has the value 1 if it is on the sheet and 0 otherwise.
- ⓑ On this understanding, when the player’s hand is raised when a wff α is called it will mean that α has the value 1, and when the player’s hand is kept down when α is called it will mean that α has the value 0.
- ⓒ A formula will be successful in a PC-setting iff it has the value 1 for the corresponding assignment of truth-values to its variables.
- ⓓ And a formula will be PC-successful iff it is has the value 1 for every PC-assignment. I.e., the PC-successful wff are precisely those which are PC-valid.
⑧ Since for any wff α containing n variables we need only consider sheets which contain a selection (possibly all or possibly none) of those n variables (for clearly the responses to variables not in α cannot affect the response to α), we can set out all the relevantly different PC-settings on
(6) Testing for Validity: (i) the truth-table method
① In this method of testing a PC formula, α, for validity, all possible PC value-assignments, i.e. all assignments of truth-values to the propositional variables in α, are tabulated, and for each such value-assignment, the basic truth-tables for the operators are used to calculate the truth-value of α as 1 or 0. The result is a column of 1s and/or 0s.
② This column is known as the truth-table of the wff. If and only if it consists entirely of 1s, the wff is valid.
③

(7) Testing for Validity: (ii) the Reductio method
① The Reductio method enables us to find such a value-assignment if there is one.

(8) Some valid wff of PC

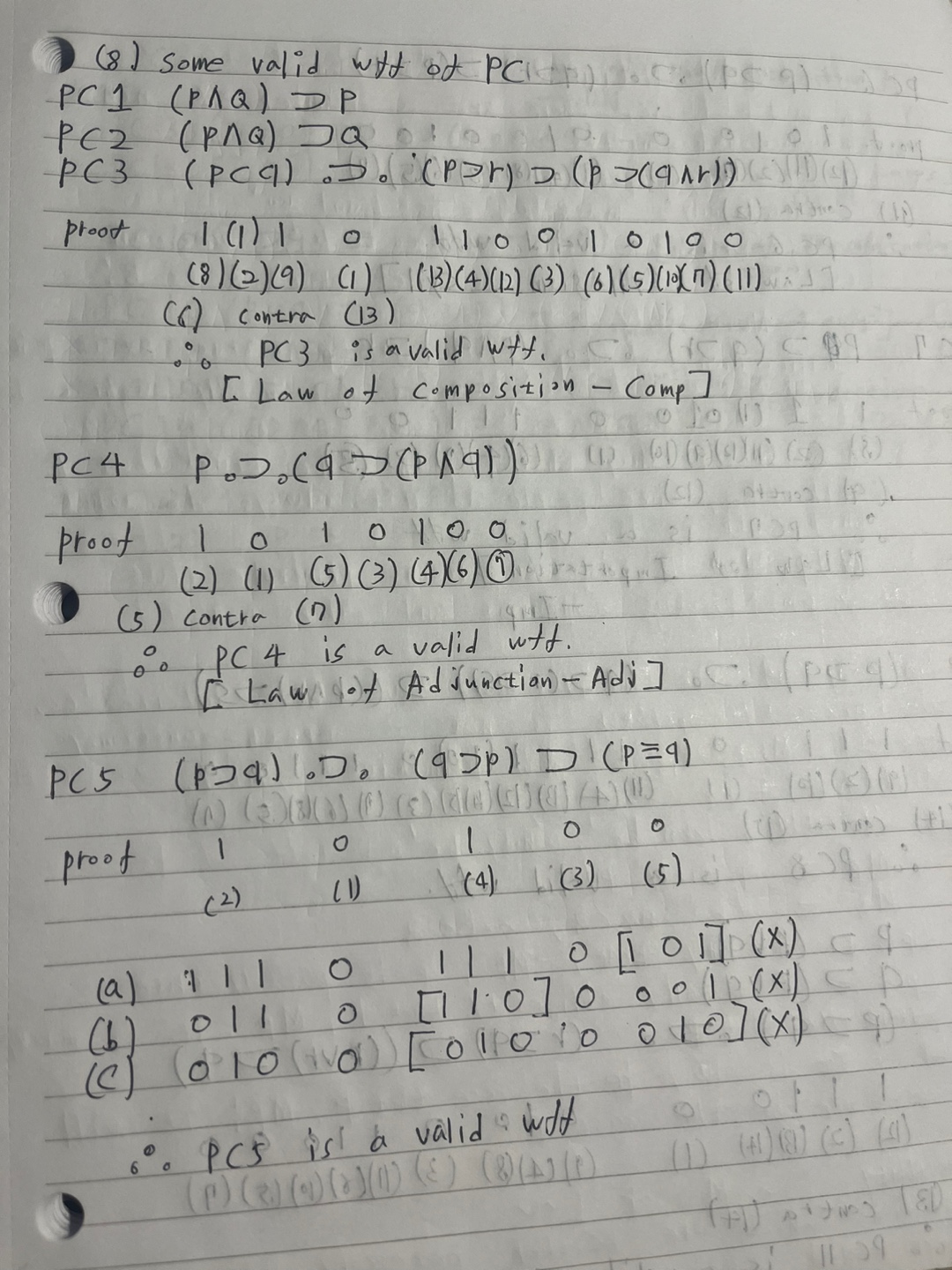

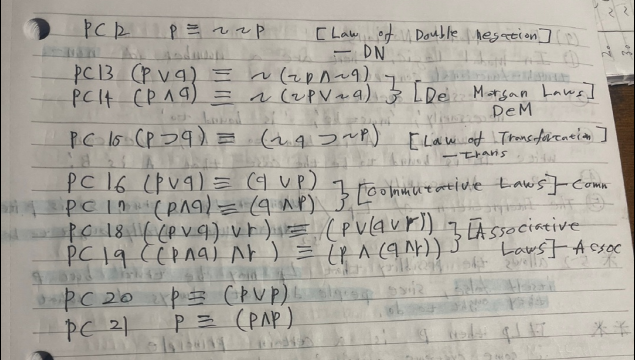
'Logic > Modal Logic' 카테고리의 다른 글
| Chapter 2. The System T (0) | 2024.01.03 |
|---|---|
| Chapter 2. The System K (K5-K9, and K*) (0) | 2024.01.02 |
| Chapter 2. The System K (K1-K4) (0) | 2024.01.02 |
| Chapter 2. An Axiomatic Basis for a Logical System (0) | 2024.01.02 |
| Chapter 1. Basic Modal Notions (0) | 2024.01.02 |