G.E. Hughes & M.J. Cresswell, A New Introduction to Modal Logic, London and New York: Routledge, 1996, pp. 33-36.
(4) L and M
① K5 Lp ≡ ~M~p
K5: Lp ≡ ~M~p
Proof
1. p ≡ ~~p PC12 (DN)
2. Lp ≡ ~~Lp 1[Lp/p]
3. Lp ≡ ~~L~~p 2 × 1 × Eq
4. Lp ≡ ~M~P Def M Q. E. D.
※ Clearly K5, by Eq, will entitle us to replace L by ~M~ anywhere in a theorem; and by Def M we may replace M anywhere in a theorem by ~L~.
② The rule of L-M Interchange (LMI)
- (a) in any sequence of adjacent monadic modal operators (Ls and Ms) in a theorem, L may be replaced by M and M by L throughout, provided that a ~ is either inserted or deleted both immediately before and immediately after the sequence. (Thus LM may be replaced by ~ML~, ~LLL by MMM~, MLLM~ by ~LMML, and so forth.)
- (b) We shall now establish that this rule holds in K.


- (c) Note that the sequence to which we apply LMI may have only a single member. Applications of K5 and Def M are thus themselves applications of LMI, and when convenient we shall indicate them too by ‘× LMI’. Note too that there is nothing to prevent us applying LMI only to part of a sequence; e.g. we may apply LMI to the first three operators in LMMLM, leaving the last two unaltered, and thus obtain ~MLL~LM.
③ K6 M(p ∨ q) ≡ (Mp ∨ Mq)
K6: M(p ∨ q) ≡ (Mp ∨ Mq)
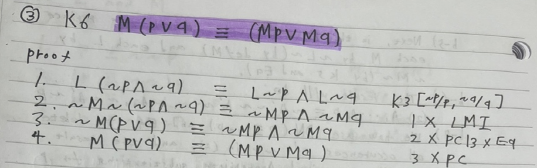
K6 expresses the same kind of principle for possibility and disjunction as K3 does for necessity and conjunction; it may be called the Law of M-distribution.
④ K7 M(p ⊃ q) ≡ (Lp ⊃ Mq)
K7: M(p ⊃ q) ≡ (Lp ⊃ Mq)

⑤ DR 3


※ Note that by repeated applications of DR1 and/or DR3 we can prefix any sequence of modal operators to both sides of an implicative theorem.
⑥ K8 M(p ∧ q) ⊃ (Mp ∧ Mq)
K8: M(p ∧ q) ⊃ (Mp ∧ Mq)

⑦ K9 L(p ∨ q) ⊃ (Lp ∨ Mq)
K9: L(p ∨ q) ⊃ (Lp ∨ Mq)

⑧ K* (Lp ∧ Mq) ⊃ M (p ∧ q)
K*: (Lp ∧ Mq) ⊃ M (p ∧ q)

'Logic > Modal Logic' 카테고리의 다른 글
| Chapter 2. The System D (0) | 2024.01.03 |
|---|---|
| Chapter 2. The System T (0) | 2024.01.03 |
| Chapter 2. The System K (K1-K4) (0) | 2024.01.02 |
| Chapter 2. An Axiomatic Basis for a Logical System (0) | 2024.01.02 |
| Chapter 1. Basic Modal Notions (0) | 2024.01.02 |