G.E. Hughes & M.J. Cresswell, A New Introduction to Modal Logic, London and New York: Routledge, 1996, pp. 43-45.
(6) The System D
① Interpretation of L as expressing obligationess (moral necessity)
- (a) Lp ⊃ Mp is not valid in this system, since when it will then mean is that whatever ought to be the case is in fact the case.
- (b) D Lp ⊃ Mp (Denotic Interpretation)
Lp: It is obligatory that P
Mp: It is permissible that P
Lp ⊃ Mp: Whatever is obligatory is at least permissible, which souns resonable enough.
- (c) The System D
D = K + D (Lp ⊃ Mp)
② Translation into quantification theory

③ D1 M(p ⊃ p)
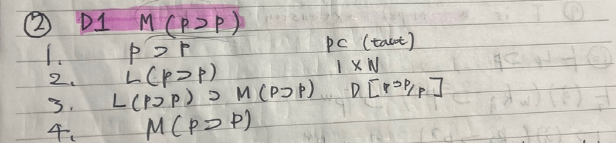
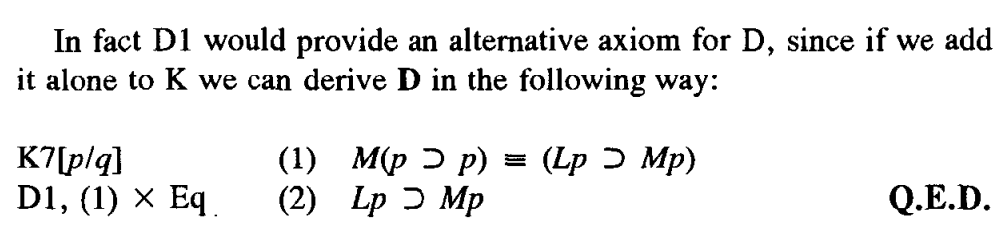
④ It is worth noting that if any wff α is a theorem of D, then so is Mα.
1. Suppose α is a theorem of D
2. Lα 1 × N
3. Lα ⊃ Mα D
4. Mα 2, 3 MP
⑤ If any system which is an extension of K has any theorems of the form Mα, that system contains D.
1. Suppose Mα is a theorem of such a system
2. α ⊃ (p ⊃ p) PC[α/q]
3. Mα ⊃ M(p ⊃ p) 2 × DR3
4. M(p ⊃ p) 1, 3 MP
⑥ D is not a theorem of K, and T is not a theorem of D. D, however, is a theorem of T.
1. Lp ⊃ p T
2. p ⊃ Mp T1
3. Lp ⊃ Mp 1, 2 Syll
∴ T is a proper extension of D
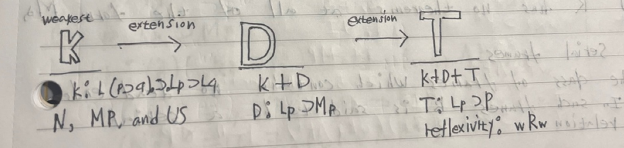
⑦ Dead Ends
- (a) There is nothing in our definition of ‘frame’ to prevent there being some worlds in a frame which cannot see any world in that frame at all.
- (b) the rule [VL] says that Lα is true in a world w iff α is true in every world that w can see, and we interpret this to mean that if there is no world at all that w can see, then Lα is (trivially) true in w, no matter what wff α may be (even if it is p ∧ ~p).
- (c) ~Lα ≡ M~α, and by [VM] any wff of form Mα can be true in w only if there is some world that w can see.
∴ ~Lα is always false in a dead end.
- (d) if a frame contains any dead end w, then D is not valid on that frame.
D: Lp ⊃ Mp
≡ ~Lp ∨ Mp
in a dead end, Lp is 1, Mp is o
V(Lp, w)=1, V(Mp, w)=0
- (e) K has no theorems at all of the form Mα
⑧ Serial frames
- (a) The class of frames which contain no dead ends.
- (b) In such frames R is said to be a serial relation.
- (c) <W, R> is a serial frame iff for every w ∈ W, there is some w' ∈ W such that wRw'.
- (d) D must be valid on every serial frame.

⑨ D-validity
a wff is D-valid iff it is valid on every serial frame.
⑩ T is a proper extension of D

'Logic > Modal Logic' 카테고리의 다른 글
| Chapter 3. The System S4 (0) | 2024.01.03 |
|---|---|
| Chapter 3. Iterated Modalities (0) | 2024.01.03 |
| Chapter 2. The System T (0) | 2024.01.03 |
| Chapter 2. The System K (K5-K9, and K*) (0) | 2024.01.02 |
| Chapter 2. The System K (K1-K4) (0) | 2024.01.02 |