Landini, Gregory (2012). Frege's Notations: What They Are and How They Mean. London and Basingstoke: Palgrave-Macmillan. [1-14]
※ Author’s Note on the Use of Modern Logical Notations
The book endeavors to explain Frege’s notations in terms of modern notations. It is therefore worth making a few comments on the modern notations used in the book that might not be familiar to readers. In addition to brackets, dots are used for punctuation to help avoid a proliferation of brackets. I always use dots symmetrically for ease of reading. Thus, for example,

I also allow subscripting a variable to the logical particles → and ↔ as convenient notation for universal quantification. For example,

Letters such as F and G, ϕ, ψ are predicate variables of the object language, while letters A, B are schematic for well-formed formulas. The sign ∀ is our universal quantifier and the sign ∃ is our existential quantifier. The book does not follow Frege in adopting Roman letters in addition to Gothic letters. As we shall see, the book maintains that this is a distinction without a difference. The book does follow Frege in using letters ξ, Φ, Ψ as parametric [매개변수의] letters which are not part of Frege’s intended formal languages. This is a distinction with a very important difference.
Introduction
1. Main Goal: Rehabilitating Frege's Formalism
A revolution was on its way in logic whose implications for philosophy would be every bit as momentous as the Copernican revolution in physics.
Boole’s pioneering Laws of Thought (1854) offered a new algebraic approach to logic, and together with Peirce’s work and Schröder’s three volume Vorlesungen über die Algebra der Logik (1890–1905), this algebraic tradition marks a remarkable advance over Aristotelian and medieval methods. But when it comes to the revolution in logic, it is the mathematician Gottlob Frege who played the role of Copernicus.
Frege’s work can be separated into three basic phases:
Begriffsscrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (1879),
Die Grundlagen der Arithmetik: eine logische-mathematische Untersuchung über den Begriff der Zahl (1884)
Grundgesetze der Arithmetic (vol. I 1893, vol. II 1903).
Main thesis: We endeavor to turn this on its head – Frege’s popular writings must be understood in terms of the formal deductive systems embedded in his notations.
His philosophy, and indeed, central derivations of theorems of his systems, cannot be recovered by investigating what might have been thought to be straightforward translations of his notations into those of a modern predicate calculi.
Why it is that differences are so important between a modern predicate logic of first or higher order and a formal system of logic that is a function-calculus (a phrase which we shall use synonymously with “function-script”).
2. Function
Frege adopts functions as primitive indefinable entities.
2.1 Defining a Function through a Relational Sign
The notion of a “function” used by philosophers today, however, has changed from its original mathematical meaning. Many today identify functions with relations R that have the special feature that

A function relates each element of a set with exactly one element (not 2 or more) of another set (possibly the same set).

Some relations do not have this feature. But those that do are said to be “functional.” Here we use the arrow → sign for “if ... then.” We shall subscript the arrow to conveniently abbreviate universal quantification. Thus, the above can be written as

This says that for all x, y, and z, if x bears relation R to y and x bears relation R to z, then y = z. Now consider the formula

This says that the unique entity to which x bears R is y.
Here the expression “R ‘x” is a term and not a formula. Only a term can flank the identity sign.
There are different ways to introduce function signs such as “R ‘x” to facilitate derivations in a formal system. One method is to employ Russell's theory of definite descriptions. A more artificial yet convenient method is to adopt an axiom such as the following:


This axiom supports the elimination of the sign “R ‘x” from all expressions, and it is non-creative (i.e., any theorem proved with the sign “R ‘x” can be proved without it).
This approach is called the “chosen object view,” for in all cases where the relation R is not functional, the axiom assigns a chosen object Δ to be the referent of “R ‘x ‘ .”
Thus, with the axioms for identity, we readily arrive at the familiar theorem
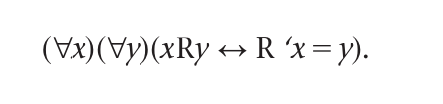
2.2 Frege's notion of a function
It is absolutely essential to understand that this is not Frege’s approach. Frege’s work does not identify functions with special relations of this sort. Frege’s “fx” must not, therefore, be conflated with “R ‘x.” For Frege, the ontology of functions, not relations, is the foundation of logic (and arithmetic and analysis).
This difference in orientation is of utmost [극도로] importance. Yet it has been widely neglected. It is easy to become wholly blind to it. The very expression “function calculus” has been corrupted by some followers of Alonzo Church, who, slighting all important differences between a term “fx” and a formula “Fx,” make no distinction between a function calculus and a predicate calculus! But more charitably, perhaps this neglect is due to the belief that the difference is ultimately insignificant for understanding Frege. On this view, the achievements of Frege’s work can adequately be represented without respecting the functions-as primitives orientation of his work. This book will show that this belief is mistaken. It took years for me to see this myself. There seemed no point in learning the details of Frege’s strange notations and proofs. It appeared to be enough to be able to translate his theorems, ignoring the odd eccentricities of his systems, into the normal language of a predicate calculus.
Consider, for example, Frege’s definition of u ^ v. Frege has
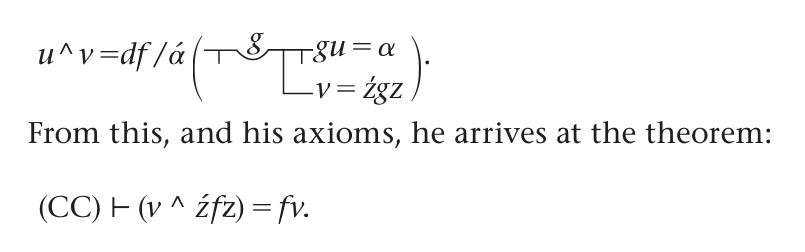
Why not just replace Frege’s function sign f with the predicate sign F and replace his expression z'fz with the class sign {z: Fz} for the class of all and only objects that exemplify the property F? This would have us simply replace Frege’s theorem with
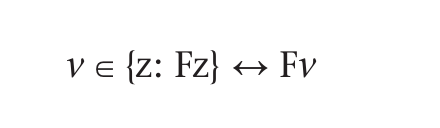
and avoid the troubles of his orientation to functions. Where ∈ is understood as “class membership”, it may seem that we can work with the following translation
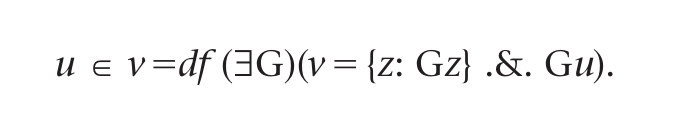
Why, then, go to the trouble of working in Frege’s archaic system?
2.3 The extension of a relation
Readers of Frege will first discover a reason for going to the trouble when they encounter Frege’s treatment of the mathematical notion of the extension of a relation.
There was a serious problem at the turn of the last century concerning what is to be the extension of a relation, R, say of two terms. Relations order their terms. For example, if R is the relation “loves”, xRy is not always equivalent to yRx. In 1912/1914, Wiener and Kuratowski found ways of capturing order in the extension of a relation. Define as follows:
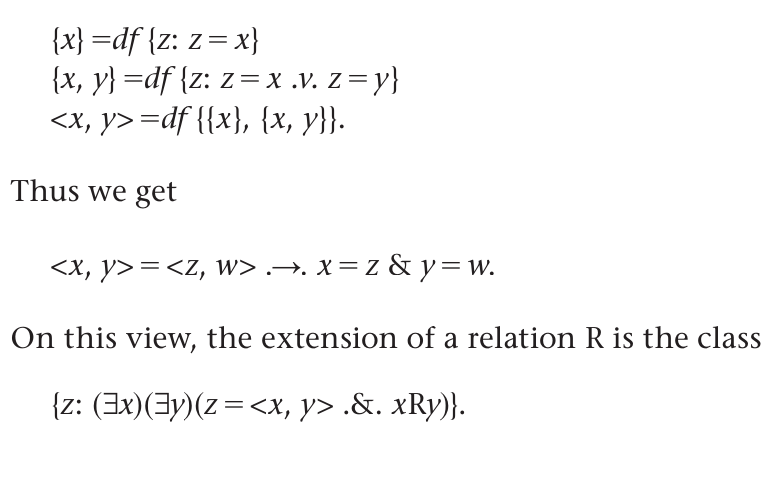
The Wiener–Kuratowski construction finds a class that preserves order. Frege’s approach does not find a class to represent the ordering that is given with relations. Frege’s solution is to replace the function fξ in (CC) by the function

For this to be intelligible, (CC) has to be an identity, and “fz” has to be a “function term”, not a formula “Fz.” There is no hope of under standing Frege’s approach otherwise. It is not that scholars in the past haven’t noticed such matters. It is rather that they have assumed that they never play a significant role in any of Frege’s philosophical or math ematical achievements. His solution to the problem of the extension of a relation, since it relies on the strange details of Frege’s formal func tion-calculus is, ipso facto, regarded as something that is not among his achievements!
Anyone with a background in logic and struggling to understand Frege’s own notations will immediately notice the archaic features of his formal system. The above is but one of many examples to be dis cussed in this book. Most interpretations account for this by explaining that Frege regarded sentences as names for truth-values (the True and the False). The working assumption has been that the odd features of some of Frege’s proofs are due to his treatment of sentences as names. These oddities, it is thought, can be safely ignored because they do not have any impact on Frege’s achievements in logic.
The prevalent attitude, therefore, is to translate away the oddities of Frege’s function calculus. With this attitude, Frege’s thesis that zΦz is a heterogeneous function from functions g to objects g zgz seems just unnecessary and archaic. Indeed, since g ξ can be any function sign, including x2, his approach allows the bewildering case of z(z2). If we don’t take this seriously, we can imagine that this feature of his system can safely be ignored in a charitable characterization of his work. But if we do take it seriously, we can immediately see that Frege does not have the modern notion of a class (or set) in mind. It turns out that taking it seriously is precisely what yields fruitful new perspectives for understanding Frege’s philosophy of arithmetic. In Frege’s view, zgz is to be understood only in terms of its being an object that is correlated uniquely with the function g ξ. These are function correlates, not classes. This thesis of correlation, long championed by Nino Cocchiarella,2 was largely ignored in the literature on Frege’s philosophy of arithmetic as an incidental artifact of Frege’s archaic system for logic. But as we shall see, the thesis of correlation is the centerpiece of Frege’s theory that cardinal numbers are those objects properly correlated with second-level numeric concepts.
Correlation is not an artifact of Frege’s system – something safely lost in translation. Quite the contrary, correlation shows precisely why Basic Law V of the Grundgesetze is not a case of definition by abstraction and why Frege rejected Hume’s Principle. In the orthodox translation, Hume’s Principle says that the number of F’s the number of G’s if and only if F’s correspond one-to-one with G’s. Basic Law V says that the f extension of F the extension of G if and only if all and only F's are G's. f The two appear to be alike as abstraction principles. Viewed in trans lation, it seems impossible to discern how Frege could favor one over the other as a foundation for his logicism. Viewed from the perspec tive of the formal system of the function calculus of the Grundgesetze, however, an entirely different perspective emerges. Basic Law V has the form
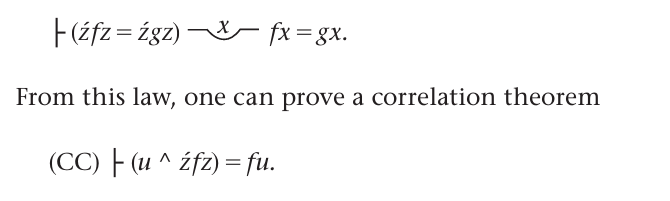
To do the work set out for it, this theorem has to be an identity (not a biconditional). Thus, to prove it, we cannot alter Basic Law V to reformu late it with biconditionals without undermining its import in the system. The clause
in Basic Law V is essential. But this is ill-formed in a predicate language.
'Analytic > History of Analytic' 카테고리의 다른 글
| 전기 비트겐슈타인과 말할 수 없는 것의 형이상학 (0) | 2024.11.08 |
|---|---|
| Frege and the Distinction between Terms and Formulas (0) | 2024.10.30 |
| 『논리-철학 논고』의 말할 수 있는 것 (0) | 2024.07.11 |
| Aspect-Blindness (Philosophy of Psychology §257) (0) | 2024.05.09 |
| On the Tractarian Concept of 'nonsense (Unsinn)' (0) | 2024.02.28 |