2024-2 Frege and Russell Midterm Exam
#2) Explain why so many interpreters have held that Frege’s formal work breaches the distinction between term and wff. Find passage(s) in “On Sense and Reference” that suggest that Frege held that a declarative sentence names a truth-value. Explain how one can save Frege from this breach by interpreting his view as introducing characteristic functions for properties and relations. In particular, take the case of the identity sign “x=y” which looks like a wff (in modern language) and compare it to the function term “=(x, y)” that Frege intends. Find passages in Grundgeseze that support the view. How does Sluga explain informativity of true identity (i.e., sameness of conceptual content ≣) while maintaining that the two sides of a true identity statement have the same sense. (Hint: syntactically different expressions occur on the two sides flanking the ≣ sign.) Compare Dummett’s understanding of Frege’s view on the informativity of identity “a = b” of Grundgesetze (having made the sense-reference distinction) as opposed to “a ≣ b” of the Begriffsschrift and Grundlagen where the sense-reference distinction hadn’t yet been made.
(A) To articulate the problem, I shall begin by introducing the distinction between a term and a formula. In modern logic, the distinction between a term and a well-formed formula (wff) is crucial for constructing a formal language for first order predicate logic. Roughly speaking, we use terms to name something, whereas formulas, by contrast, are used to say something. According to one general explanation, a term is either an individual constant, an individual variable, or an n-place function symbol followed by n terms, and nothing else is considered a term (Hunter 1971: 137). If no variable occurs in a term, the term is closed; otherwise, it is an open term.
According to Hunter, “a formal language can be identified with the set of its well-formed formulas” (Hunter 1971: 4). Undoubtedly, the nature of a formal language is that every well-formed formula must be definable without any reference to its interpretation. A formal language thus requires “a set of formation rules determining which sequence of symbols from his alphabet are wffs of his language” (Hunter 1971: 4). In other words, a breach of following formation rules results in ill-formed formulas.
Now, the formation rules in the standard quantification theory are as follows:
1. Any propositional symbol is a wff and an atomic wff.
2. If F is an n-place predicate symbol and t₁,…tₙ are terms (not necessarily distinct), then Ft₁…Ftₙ is a wff and an atomic wff.
3. If A is a wff and v an individual variable, then ∀vA is a wff.
4. If A is a wff, then ~A is a wff.
5. If A and B are wffs, then A ⊃ B is a wff.
6. Nothing else is a wff.
(Hunter 1971: 137-138)
From this consideration, it is clear that (A ⊃ B) is well-formed insofar as both A and B are wffs. In modern logic, not only are (A ∨ B), (A ∧ B), and (A ≡ B) wffs, but their components, i.e., A and B, are wffs as well. It is also worth noting that terms combined with a relation sign can form a wff. For example, x = y is a wff, where x and y are terms; Lxy is a wff, where x and y are terms, and so on.
Now, confusion may arise when terms are combined with logical constants, or when wffs are combined with relation signs. It is without doubt illicit to say x⁴ ≡ y, where x⁴ and y are terms. x⁴ ≡ y lacks truth-conditions, since both x⁴ and y are neither true nor false in the first place (the term, ‘Socrates’ is neither true nor false, while a wff ‘Socrates was sentenced to death’ is either true or false). Likewise, if A and B are wffs, A = B is unintelligible. It is innocuous to combine two different names with the identity sign ‘=,’ since different names (e.g., the morning star and the evening star) can refer to the same thing. However, wffs do not function to refer to objects at all.
Given the fundamental significance of this distinction in modern languages, it is quite surprising that Frege was accused of breaching it. Anyways, didn’t he argue that a sentence functions to refer to objects (the True and the False) when he claimed that a sentence is a proper name? Dummett, for instance, famously referred to Frege’s mistake as a gratuitous blunder. He argues:
The identification of truth-values as the referents of sentences, taken together with the thesis that truth-values are objects, led to a great simplification in Frege’s ontology, at the price of a highly implausible analysis of language. Sentences being only a special case of complex proper names, and truth-values only a special case of objects, it follows that predicates and relational expressions are only a special case of functional expressions (unary and binary respectively), and concepts and relations only a special case of functions: concepts and relations are, in fact, just those functions, of one or two arguments, whose values are always truth-values. […] It is tragic that a thinker who achieved the first really penetrating analysis of the structure of our language should have found himself driven into such absurdities. It is not, of course, that there is anything formally wrong with imposing such a requirement upon a language, although, as we shall see, the assimilation of sentences to proper names did have a fatal effect upon Frege’s theory of meaning. It is just that Frege’s earlier departures from the forms of natural language―in particular, his notation for generality―were founded upon deep insights into the workings of language; whereas this ludicrous deviation is prompted by no necessity, but is a gratuitous blunder. (Dummett 1973: 183-184)
According to Dummett, Frege holds that a sentence is a special case of a proper name, i.e., a closed term for truth-values. As a corollary, truth-values are the referents of sentences (which are objects). At first glance, Dummett’s interpretation is buttressed by a claim made by Frege himself. In “On Sense and Reference,” Frege said:
We are therefore driven into accepting the truth-value of a sentence as constituting its Bedeutung [reference]. By the truth-value of a sentence I understand the circumstance that it is true or false. There are no further truth-values. For brevity I call the one the True, the other the False. Every assertoric [declarative] sentence concerned with the Bedeutung of its words is therefore to be regarded as a proper name, and its Bedeutung, if it has one, is either the True or the False. (Frege 1892a: 157-158)
Landini attempts to save Frege from this breach by interpreting his view as introducing characteristic functions for properties and relations. He claims that “Frege’s function-script transcribes ordinary language sentences by means of a technique of characteristic functions […] commonly used in mathematics in Frege’s day” (Landini 2012: 30). One of the common examples would be:

Recall that in the standard quantification theory, Ftₙ is a wff. On the contrary, Frege’s function sign ‘fn’ is a term. Its components, i.e., ‘n is even,’ and ‘n is odd’ are wffs (Landini 2012: 30). Thus, when Frege maintained that every declarative sentence is to be regarded as a proper name of the True and the False, what he had in mind is not that every declarative sentence is a term, but that it is component of a characteristic function ‘fn’ such that:

, where A[x₁,…,xₙ] is a wff and f(x₁,…,xₙ) is a term.
It is well known that Frege used a composite of the judgment stroke (┃) and the horizontal (―), ├, in a way that differs significantly from modern logic. In modern language, ├ is only attached to a wff and indicates that ‘A is a thesis (axiom or theorem)’ (so ‘├’ belongs to meta-language). In Frege’s notation, on the contrary, ├ belongs to object-language; it is attached to a term f(x₁,…,xₙ) to make a formula.
To elucidate Frege’s ├, we must comprehend the roles of ┃ and ― in his notation. According to Frege, “in a mere equation there is no assertion; “2+3=5” only designates a truth-value, without its being said which of the two it is.” (BLA: 37) Thus, “(2+3=5) = (2=2)” with the assumption that we knew 2=2 to be the True does not make an assertion that the sum of 2 and 3 is 5. Rather, it merely designates the truth-value of “2+3=5”’s denoting the same as “2=2” (BLA: 37). If we want to make such an assertion, an additional special sign is needed.
Accordingly, Frege first introduced a function name, ―∆, by which he means that ―∆ is the True if ∆ is the True; ―∆ is the False if ∆ is the False (BLA: 38). In other words, it is a characteristic function, expressed as follows:
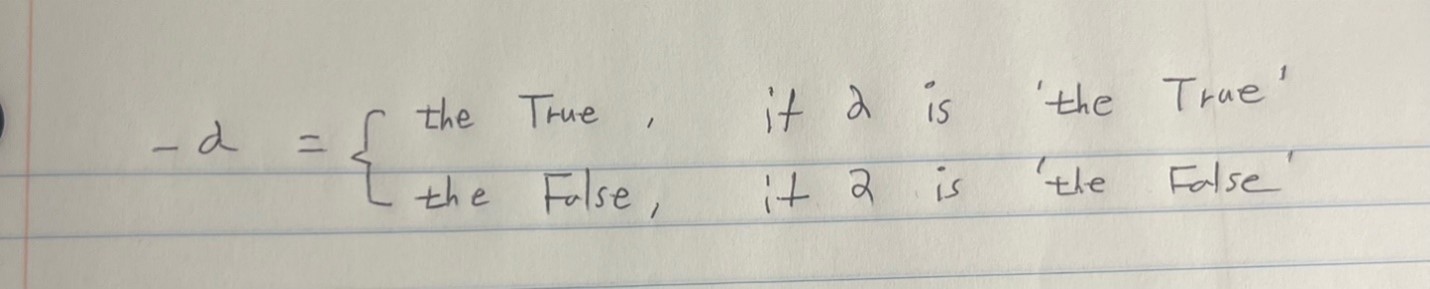
Thus, for Frege, “1² < 3” is not a wff such that “1² is less than 3” (Landini 2012: 35). It is instead a term (i.e., a characteristic function sign), expressed as follows:

This is the reason why Frege reads
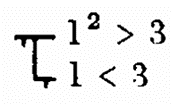
as “the truth-value of neither the square of 1’s being greater than 3 nor 1’s being smaller than 3” (BLA: 52).
For the same reason, Frege’s function term “=(x, y)” must not be confused with “x = y,” which is a wff in modern languages. “=(x, y)” can be expressed as follows:

In Frege’s notation, ┃ must be added to make an assertion (which is a wff). Only in ├ 2² = 4 it is asserted that square of 2 is 4 (BLA: 38). “Of the two signs of which “├” is composed, only the judgment stroke contains the act of assertion.” (BLA: 39). From this consideration, Landini concludes that Frege has never breached the term/formular distinction. He claims:
Taken in light of the syntax of his Grundgesetze, Frege’s point in his article “On Sense and Reference” is that sentences and well-formed formulas play a role in introducing characteristic functions. But these function signs are terms, not formulas. If this simple account is correct, it means that Frege’s formal language respects the ordinary syntactic distinction between terms and formulas (Landini 2012: 33-34).
Thus, it must be noted that only ├ =(x, y) corresponds to x = y in modern notation. Frege’s x = y is a term, not a formula. It is also worth nothing that├ =(x, y) has neither sense [Sinn] nor reference [Bedeutung]. Otherwise, Frege’s formal language would again contravene the syntactic distinction between terms and formulas. Now, if ‘=’ is a primitive function sign, and 2² and 4 are terms, then = (2², 4) is a term. We can then analyze the sense of such a term as follows:
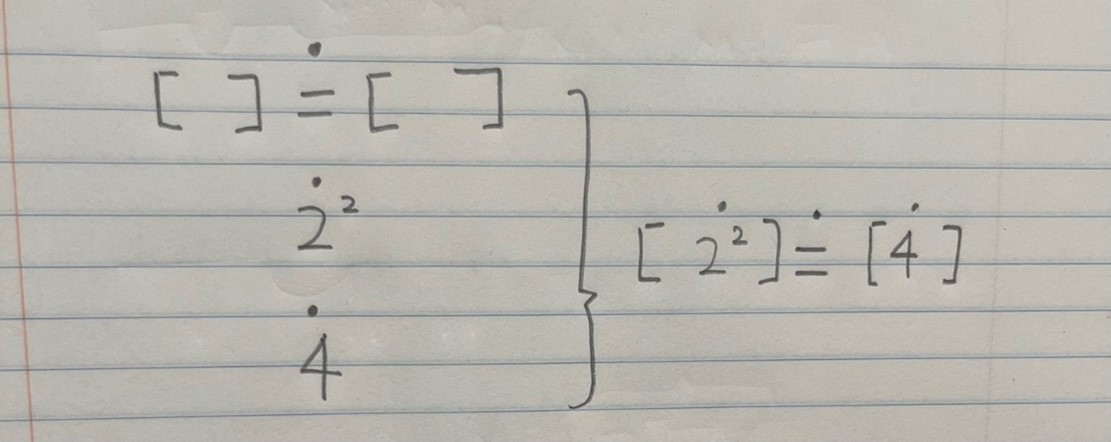
There was a debate between Sluga and Dummett regarding the determinacy of analysis of a complex sense. One might argue that our analysis of = (2², 4) is not the only one, but it can be also composed:

Sluga holds that all the three ways of decomposition are correct, as it is the mind that plays a role in decomposing a Gedanke into its parts. It is well-known that Frege, in opposition to psychologism, claims that a Gedanke belongs to the third realm, in which objective, ideal, and abstract entities exist, in order to distinguish Gedanken from mere subjective representation, Vorstellungen (FA: xxii). Sluga’s view makes Frege’s philosophy much more like Kantianism; a Gendake itself―like Kant’s notion of das Mannigfaltige―has no part at all, according to Sluga. Consequently, he argues that “syntactically different sentences may have the same Gedanke as their sense” (Landini 2012: 139). Thus, a true identity statement, say, a ≣ b can be informative even if the two sides of it have the same sense.
Dummett, on the contrary, argues that “the semantic composition of senses tracks exactly the recursive rules for the syntactic composition of the terms of the language” (Landini 2012: 135). A Gedanke, on this view, has fully determinate parts. Thus, contrary to Sluga, he argues that “a statement ├ a ≡ b of sameness of conceptual judgeable content is not informative” (Landini 2012: 48). In other words, it is not possible that a true identity statement is informative where the two sides of it have the same conceptual content.
However, the trouble with this debate is that both sides neglect Frege’s notion of comprehension. According to Landini, “Frege knew that the source of the informativity of his new logic lies in the fact that it embodies the comprehension of functions” (Landini 2012: 12).
References
Dummett, Michael (1973). Frege: Philosophy of Language. London: Duckworth.
Enderton, Herbert (1977). Elements of Set Theory. New York: Academic Press.
Frege, Gottlob (FA). The Foundations of Arithmetic. A Logico-Mathematical Enquiry into the Concept of Number. translated by J. L. Austin. New York: Harper Torchbooks, 1960.
Frege, Gottlob (BLA). The Basic Laws of Arithmetic. Exposition of the System. translated and edited by Montgomery Furth, Berkeley and Los Angeles: University of California Press, 1967.
Frege, Gottlob (1891). “Function and Concepts.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.
Frege, Gottlob (1892a). “On Sinn and Bedeutung.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.
Frege, Gottlob (1892b). “On Concept and Object.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.
Hunter, Geoffrey (1971). Metalogic: an introduction to the metatheory of standard first order logic. Berkeley, CA: University of California Press.
Klement, Kevin C. (2001). Frege and the Logic of Sense and Reference. New York: Routledge.
Landini, Gregory (2011). Russell. New York: Routledge.
Landini, Gregory (2012). Frege’s Notations: What They Are and How They Mean. London and Basingstoke: Palgrave-Macmillan.
Landini, Gregory (2022) “Stipulations Missing Axioms in Frege’s Grundgesetze der Arithmetik,” History and Philosophy of Logic, 43:4, 347-382.
Zach, Richard (2019). Sets, Logic, Computation: An Open Introduction to Metalogic. Open Logic Project.
'Analytic > History of Analytic' 카테고리의 다른 글
| 『논리-철학 논고』의 실증주의적 해석과 “형이상학의 극복” (0) | 2024.11.08 |
|---|---|
| 전기 비트겐슈타인과 말할 수 없는 것의 형이상학 (0) | 2024.11.08 |
| Landini (2012) Frege’s Notations What They Are and How They Mean (1) Introduction (0) | 2024.09.24 |
| 『논리-철학 논고』의 말할 수 있는 것 (0) | 2024.07.11 |
| Aspect-Blindness (Philosophy of Psychology §257) (0) | 2024.05.09 |