2024-2 Frege and Russell Midterm Exam
#4)

(A) In “On Sense and Reference,” Frege wrote:
Equality gives rise to challenging questions which are not altogether easy to answer. Is it a relation? A relation between objects, or between names or signs of objects? In my Begriffsshrift I assumed the latter. The reasons which seem to favour this are the following: a = a and a = b are obviously statements of differing cognitive value [Erkenntniswert]; a = a holds a priori and, according to Kant, is to be labelled analytic, while statements of the form a = b often contain very valuable extensions of our knowledge and cannot always be established a priori (Frege 1892a: 151).
Frege’s solution is now as well-known as the problem he raised―the problem of the informativity of identity. He first introduced the distinction between sense [Sinn] and reference [Bedeutung], through which what the sign designates is distinguished from its sense, wherein the mode of presentation is contained (Frege 1892: 152). In other words, a sign has both a sense and a reference domain. Frege called the sense of a sign―if it is a complete whole―Gedanke (a thought) and maintained that the reference of a sign yields, and thereby refers to, either the True or the False. If we visualize this, it would be:

Take, for example, two distinct signs: the Morning Star and the Evening Star. We have:
(1) a = a (analytic a priori) The Morning Star = the Morning Star
(2) a = b (synthetic a posteriori) The Morning Star = The Evening Star
(1) is an analytic a priori identity statement, which is a trivial case of the law of self-identity, while (2) is a synthetic a posteriori statement, to be discovered by astronomers (Klement 2001: 10). If the meaning of the Morning Star is the same as that of the Evening Star, then (1) and (2) must also have the same meaning. Thus, the fact that (2) is informative while (1) is not seems to present a puzzle. Frege’s answer is that “the Bedeutung of ‘Evening Star’ would be the same as that of ‘Morning Star,’ but not the sense” (Frege 1892a: 152). Admittedly, both the ‘Evening Star’ and the ‘Morning Star’ designate the same object, the planet Venus. However, since the ‘Evening Star’ and the ‘Morning Star’ have different senses, combining them with the identity sign makes the statement informative. Klement concisely encapsulates Frege’s solution as follows: “While the truth of an identity statement involves only the Bedeutungen of the component expressions, the informativity of such a statement involves additionally the way in which those Bedeutungen are determined, i.e., the Sinne of the component expressions” (Klement 2001: 10). If we visualize this, it would be:

Propositional attitude contexts require a more subtle and meticulous approach. Compare, for example,
(3) Jackson believes that Venus is a planet.
(4) Jackson believes that the Morning Star is a planet
It is possible that (3) is true and while (4) is false, even though “the Venus = the Morning Star” is true. To solve this, Frege suggests that “propositional attitudes such as believing, knowing, and the like, produce contexts that are “oblique” (referentially shifted)” (Landini 2012: 146). Let me illustrate this as follows:

where a is ‘the Venus,’ c is ‘the Morning Star,’ b is ‘Jackson,’ B is ‘believing,’ o is the referent of the expressions ‘a’ and the expression ‘c,’ and fx is a characteristic function such that the True, if x is a planet and the False, otherwise. I also add a dot to the sign to designate the sense of an expression. The picture allows us to identify the main problem: Jackson does not believe the True yielded by fo. Rather, he believes the sense of ‘fa’ and does not believe the sense of ‘fc,’ respectively. In a nutshell, the object of a belief is a Gedanke. So, we need to substitute the sense of an expression for its reference (i.e., truth-values) to flank the argument position. Namely,
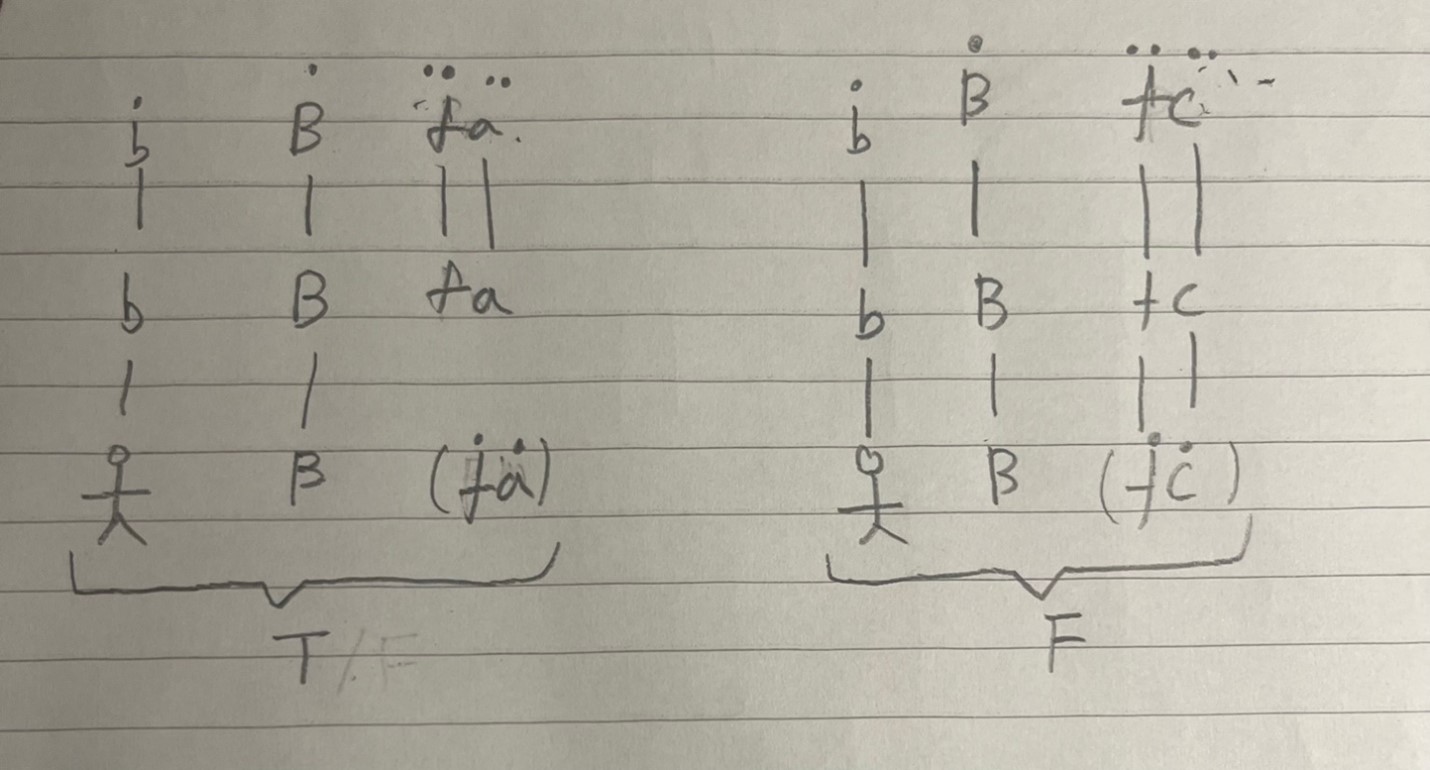
Here, the argument is a Gedanke, not a truth-value. So, f() in the sense domain now must have a double dot; it has to be a sense that picks out the sense of f() in the argument position. Likewise, c in the sense domain must have a double dot to be a sense that picks out the sense of c in the argument position. This is Frege’s doctrine of referential shift.
Of course, in ordinary language we often say:
(5) Green believes that Jackson believes that Venus is a planet
To express this, we are supposed to use triple dots as follows:
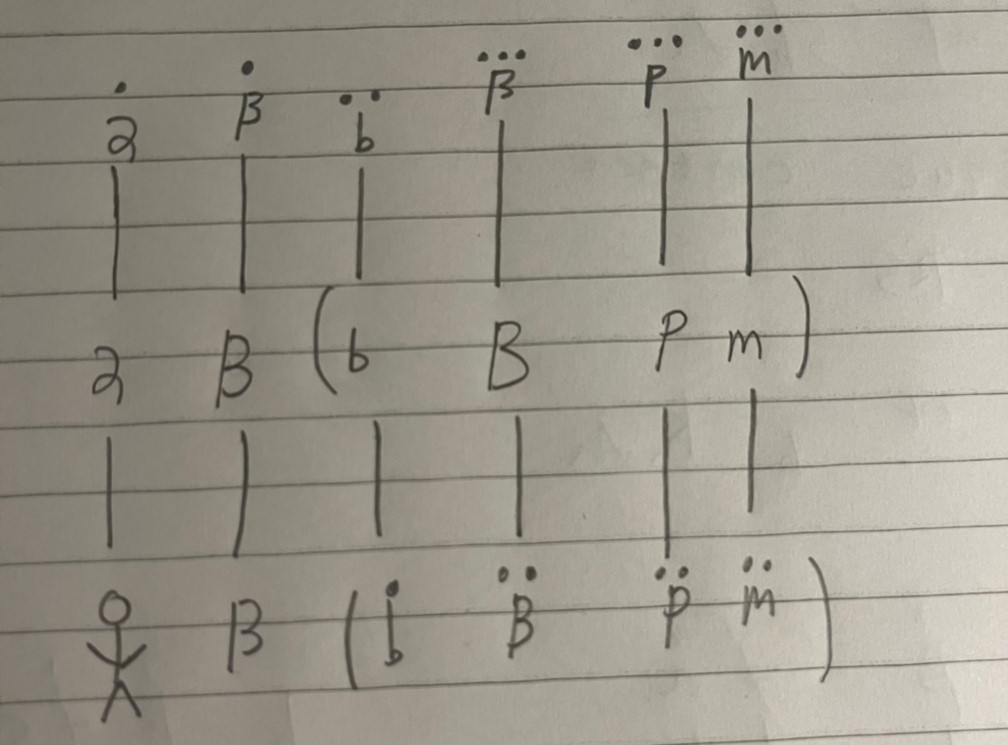
where a is ‘Green,’ b is ‘Jackson,’ B is ‘believing,’ m is ‘Venus,’ and Px is a characteristic function such that the True, if x is a planet and the False, otherwise.
Russell argued that Frege’s theory of senses yields a paradox (Landini 2012: 152). One of his attempts to show this is called the paradox of Sinn. The starting point of the paradox is Frege’s general idea that we can comprehend functions, which forms the heart of his CP Logic. The basic form of the comprehension of functions is this:
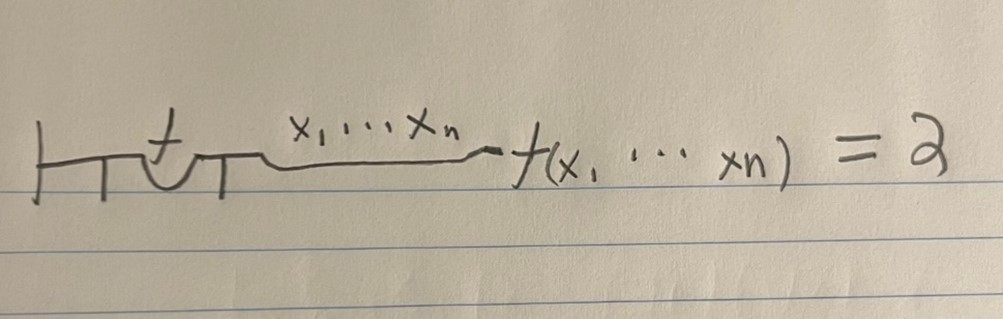
Now, for α, Russell substituted the statement that there is some function where the antecedent holds while the consequent does not.
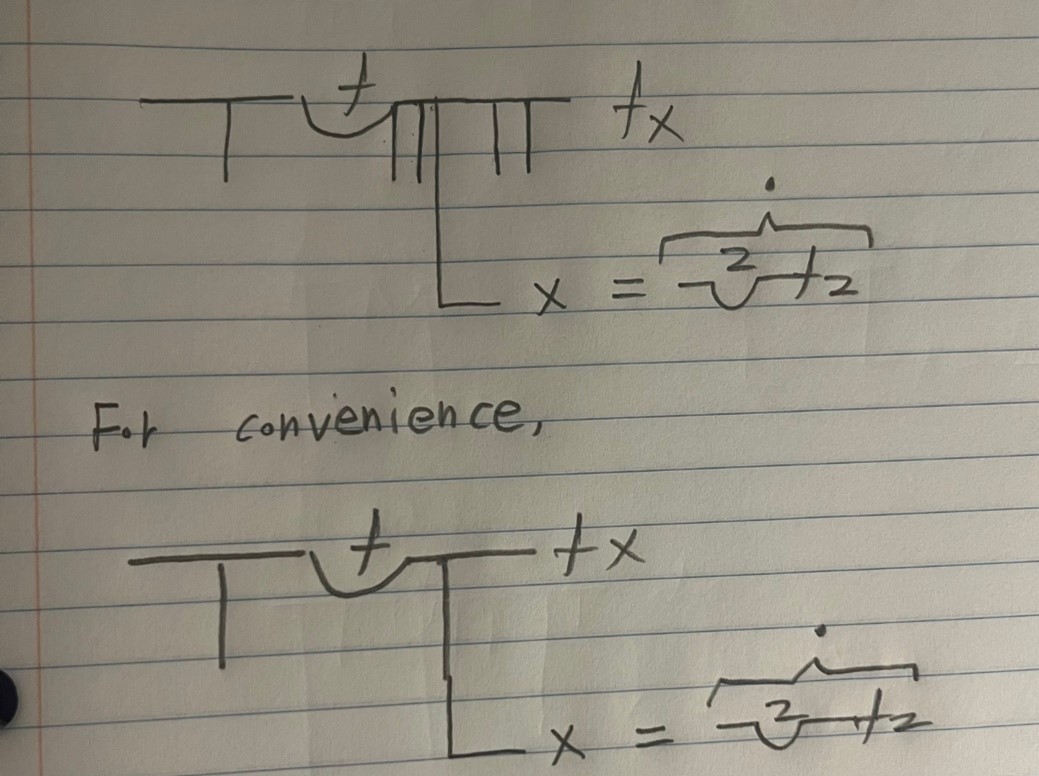
From comprehension, he derived the following:
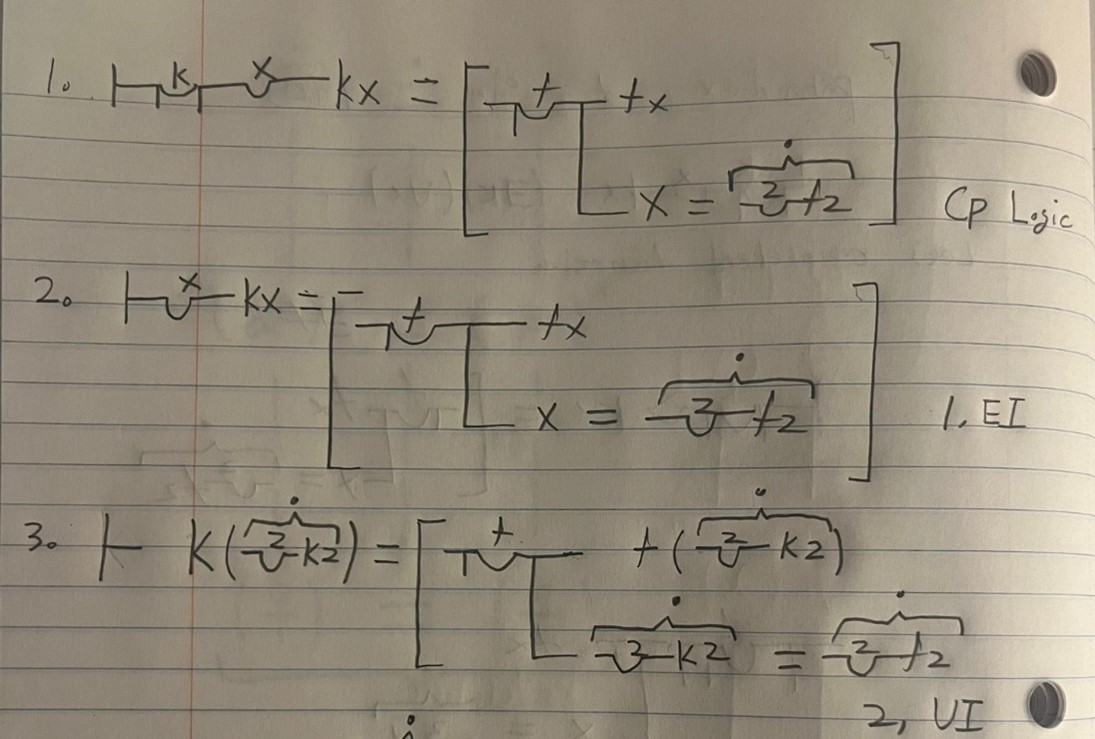
Subsequently, we can get the following conditional proof:
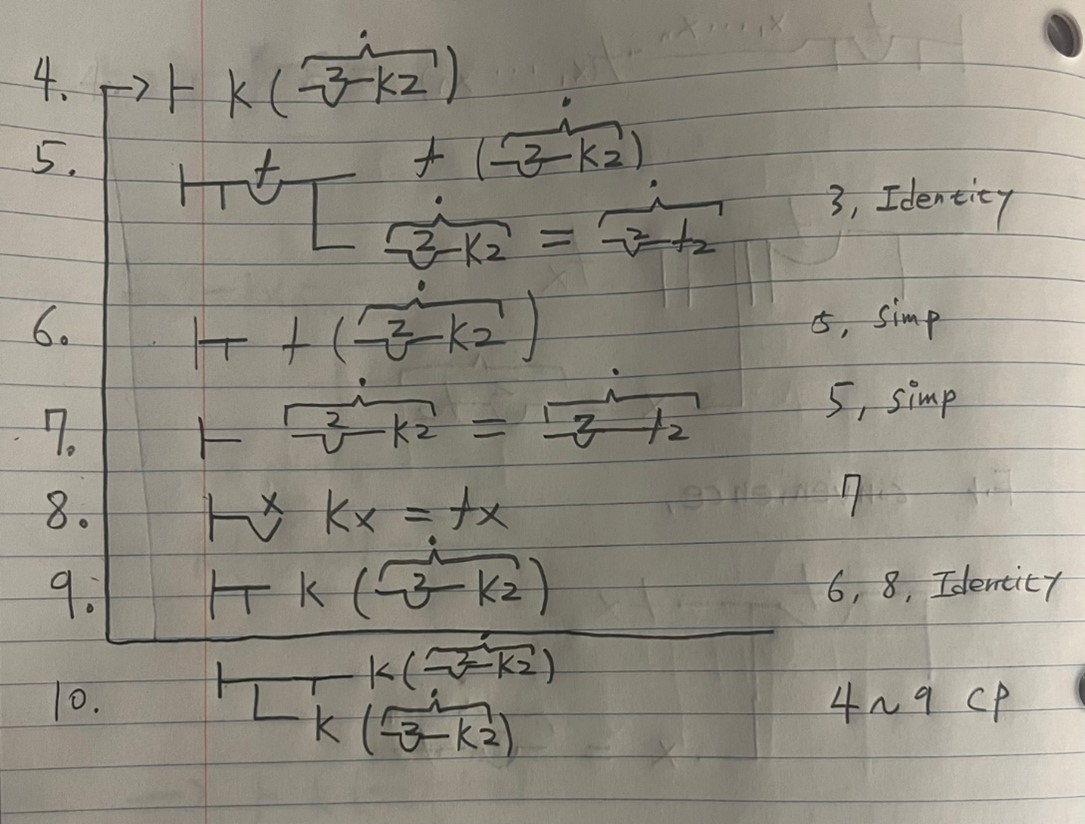
Note that Russell thought that (8) can be derived from (7); the identity of the senses ensures the identity of the functions.
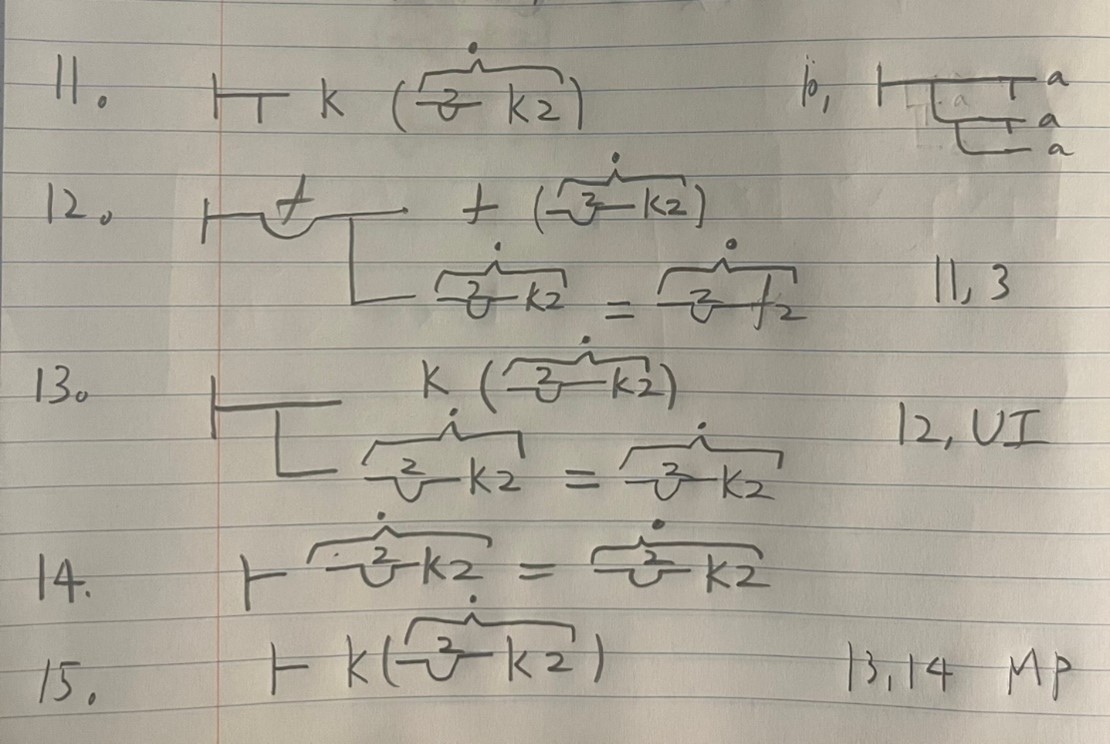
Clearly, (11) contradicts (15). Accordingly, Russell concluded that Frege’s theory of senses yields a paradox.
Frege’s reply to this is that Russell’s whole proofs are just ill-formed; Russell’s proof says that comprehension can give us contradiction if we allow quantification into the sense. Frege maintained that this is illicit. You cannot quantify into a dot as Russell did. However, one obvious implication of this reply is that you cannot quantify into the context of referential shift as well. Therefore, referential shift makes it difficult to imagine how to quantify into belief contexts.
References
Dummett, Michael (1973). Frege: Philosophy of Language. London: Duckworth.
Enderton, Herbert (1977). Elements of Set Theory. New York: Academic Press.
Frege, Gottlob (FA). The Foundations of Arithmetic. A Logico-Mathematical Enquiry into the Concept of Number. translated by J. L. Austin. New York: Harper Torchbooks, 1960.
Frege, Gottlob (BLA). The Basic Laws of Arithmetic. Exposition of the System. translated and edited by Montgomery Furth, Berkeley and Los Angeles: University of California Press, 1967.
Frege, Gottlob (1891). “Function and Concepts.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.
Frege, Gottlob (1892a). “On Sinn and Bedeutung.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.
Frege, Gottlob (1892b). “On Concept and Object.” in: The Frege Reader, edited by M. Beaney, Oxford: Blackwell, 1997.
Hunter, Geoffrey (1971). Metalogic: an introduction to the metatheory of standard first order logic. Berkeley, CA: University of California Press.
Klement, Kevin C. (2001). Frege and the Logic of Sense and Reference. New York: Routledge.
Landini, Gregory (2011). Russell. New York: Routledge.
Landini, Gregory (2012). Frege’s Notations: What They Are and How They Mean. London and Basingstoke: Palgrave-Macmillan.
Landini, Gregory (2022) “Stipulations Missing Axioms in Frege’s Grundgesetze der Arithmetik,” History and Philosophy of Logic, 43:4, 347-382.
Zach, Richard (2019). Sets, Logic, Computation: An Open Introduction to Metalogic. Open Logic Project.
'Analytic > Phil of Language' 카테고리의 다른 글
| Frege's Context Principle 2 (0) | 2024.11.07 |
|---|---|
| Frege's Context Principle 1 (0) | 2024.11.07 |
| Kripke (1980) Naming and Necessity, Lecture I (0) | 2024.10.13 |
| Wittgenstein's use theory of meaning 1 (from Philosophical Investigations §80) (0) | 2024.05.09 |
| 언어철학 정리 (0) | 2019.10.30 |